Нетранзитивные кости Эфрона
Использование нетранзитивных костей влияет на результат игры со следующими правилами:
Первый игрок выбирает игровую кость из набора.
Второй игрок выбирает одну из костей, которые остались в наборе после выбора первого игрока.
Оба игрока бросают свои кости; выигрывает игрок, у которого выпало большее число.
При использовании транзитивных костей преимущество в игре имеет первый игрок, который может выбрать кость, результат броска которой с вероятностью минимум 50 % будет больше результата броска любой другой кости из набора. В случае же использования набора нетранзитивных костей преимущество получает второй игрок, который, независимо от выбора первого игрока, может выбрать из оставшихся костей такую, бросание которой с вероятностью более 50% превысит результат первого игрока.
Кости Эфрона — набор из четырёх нетранзитивных костей, изобретенный Брэдли Эфроном.
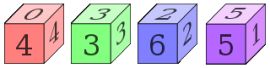
Четыре кости $A$, $B$, $C$, $D$ имеют на своих гранях следующие числа:
| $A:$ | 4, | 4, | 4, | 4, | 0, | 0 |
| $B:$ | 3, | 3, | 3, | 3, | 3, | 3 |
| $C:$ | 6, | 6, | 2, | 2, | 2, | 2 |
| $D:$ | 5, | 5, | 5, | 1, | 1, | 1 |
Результат броска каждой из кости из набора больше результата бросания следующей кости с вероятностью $2/3$:
${\displaystyle P(A>B)=P(B>C)=P(C>D)=P(D>A)={2 \over 3}}$
Результат бросания кости $B$ определен заранее; кость $A$ превысит этот результат в $2/3$ случаев, поскольку числа на четырёх из шести его граней больше.
Аналогично, кость $B$ превысит результат $C$ с вероятностью $2/3$, поскольку у $C$ только на двух гранях числа большие.
$P(C>D)$ согласно результатам составления условных вероятностей двух событий:
При бросании $C$ выпадает $6$ (вероятность $1/3$); $C$ дает больший результат, независимо от результата бросания $D$ (вероятность $1$).
При бросании $C$ выпадает $2$ (вероятность $2/3$); $C$ дает больший результат, за исключением получения $5$ при бросании $D$ (вероятность $1/2$).
Суммарная вероятность выигрыша $C$, таким образом, составляет:
${\displaystyle \left({1 \over 3}\times 1\right)+\left({2 \over 3}\times {1 \over 2}\right)={2 \over 3}}$.
Аналогичным образом вероятность выигрыша при бросании $D$ по сравнению с бросанием $A$ составляет:
${\displaystyle \left({1 \over 2}\times 1\right)+\left({1 \over 2}\times {1 \over 3}\right)={2 \over 3}}$.
Четыре кости из набора Эфрона, впрочем, имеют разные вероятности выигрыша в игре против кости, выбранной случайным образом из оставшихся трех.
Согласно расчётам выше, бросание кости $A$ дает больший результат, чем бросание кости $B$, в двух третях случаев. Впрочем, $A$ может победить $D$ только в каждом третьем случае. Вероятность же лучшего результата при бросании $A$ по сравнению с бросанием $C$ составляет $4/9$ (на $A$ должно выпасть $4$ и на $C$ должно выпасть $2$). Таким образом общая вероятность получения большего числа при бросании $A$ , чем при бросании другой кости, выбранной случайным образом:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{4 \over 9}\right)={13 \over 27}}$.
Аналогично, $B$ побеждает $C$ с вероятностью $2/3$ и может победить $A$ в $1/3$ случаев. Вероятность для кости $B$ дать при бросании результат больший, чем при бросании кости $D$, составляет $1/2$ (вероятность выпадения $1$ на кубике $D$). Таким образом, вероятность победы $B$ над другой костью из набора:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{1 \over 2}\right)={1 \over 2}}$.
Кость $C$ побеждает $D$ в двух третях случаев и имеет вероятность $1/3$ выигрыша у кубика $B$. Вероятность её выигрыша у кубика $A$ составляет $5/9$. Совокупная вероятность победы $C$ над выбранным случайным образом «соперником»:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{5 \over 9}\right)={14 \over 27}}$.
Наконец, $D$ в $2/3$ случаев побеждает $A$ и в $1/3$ случаев побеждает $C$. Вероятность, что результат броска этой кости превысит результат бросания $B$, составляет $1/2$ (вероятность выпадения $5$ на $D$). Поэтому $D$ даст результат, больший, чем у выбранной случайным образом кости с вероятностью:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{1 \over 2}\right)={1 \over 2}}$.
Таким образом, кость $C$ является наилучшей из набора с точки зрения вероятности выпадения числа, большего чем результат бросания любой другой кости из набора. Для неё такая вероятность составляет $0,5185$. Кость $C$ также характеризуется наибольшим математическим ожиданием результата бросания — $31⁄3$ (для $A$ оно составляет $22⁄3$, а для $B$ и $D$ равно $3$).
Хомячковый рай. Уйти и потеряться:
- Ваш комментарий к статье:
- Правила комментирования:
-
-
- Все поля формы обязательны для заполнения.
- e-mail не публикуется.
- Содержание комментариев, оставленных на опубликованные материалы, является мнением лиц, их написавших, и не обязано совпадать с мнением Администратора, никоим образом не ответственного за выводы и умозаключения, могущие возникнуть при прочтении комментариев, а также любые версии их истолкования.
- Однозначно не подлежат публикации комментарии:
- - содержащие оскорбления любого вида (личного, религиозного, национального...);
- - включающие неуместные теме поста ссылки, в том числе спамовые;
- - нарушающие положения законодательства РФ.
- Факт оформления Вами комментария является безоговорочным принятием этих условий.