Взлёты и падения чисел-градин

| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 3 · МАРТ 1984 · С. 102-107 |
БРАЙАН ХЭЙЕС
Пешеход, делающий три шага вперёд и два назад, хотя и не быстро, но всё же доберётся до цели. А вот в одной любопытной нерешённой задаче из теории чисел утверждается, что при таком передвижении достижение цели весьма сомнительно. Задача формулируется так. Возьмём произвольное целое число N больше нуля (любое натуральное число). Если оно нечётное, умножим его
Если задано конкретное N, то для ответа на поставленные вопросы достаточно обычной арифметики. Например, начав с нечётного числа 27, следующим получим значение
Трудность задачи заключается не в выписывании последовательности для данного N, а в нахождении общего решения, которое годилось бы для всех исходных значений N. Такое общее решение пока не получено. Было испробовано огромное количество чисел, и все они вели себя одинаково, но ещё никто не смог доказать, что так же будет с любым целым числом. Из нерешённых задач теории чисел - эта едва ли самая важная, но она одна из тех, что вызывают сильную досаду. И описание вычислительной процедуры, и её выполнение чрезвычайно просты, но понять, к чему она может привести, невероятно трудно.
На примере этой задачи особенно хорошо видны как польза компьютера при вычислениях, так и ограниченность его возможностей. С небольшими целыми числами можно справиться самим, а далее для вычислений понадобится механический помощник. Им может быть любая машина, даже небольшой программируемый калькулятор. В области же очень больших чисел такая работа под силу только самым мощным ЭВМ. Когда же ставятся более глубокие вопросы, уже не поможет никакой компьютер. Основное назначение ЭВМ - быть подспорьем в математическом эксперименте: строить примеры и контрпримеры. Для описания же закона, по которому N изменяет свои значения, нужна не числодробилка, а скорее механический <доказыватель теорем>.
Если к произвольному целому числу N многократно применять описанные преобразования, то какого результата следует ожидать? На этот счёт есть три интуитивные гипотезы.
В первой гипотезе рассуждаем так. Имеется равное количество чётных и нечётных чисел, так что в любой длинной последовательности вычислений чётные и нечётные N будут появляться одинаково часто. Нечётное N увеличивается втрое (чуть больше), а чётное уменьшается всего лишь вдвое. Следовательно, по мере роста числа итераций значение N будет бесконечно возрастать. За каждую итерацию N будет в среднем увеличиваться на
Вторая гипотеза основана на тезисе <Чем выше заберёшься, тем ниже скатишься>. Справедливость этой мысли подкрепляется тем реальным фактом, что стoит в вычислениях получить точную степень двойки, как последовательность неудержимо скатится
Третья гипотеза по форме схожа со второй, но приводит к иному выводу. Замечено, что как только вычисления меняют направление, скажем после ряда чётных чисел появляется нечётное, мы вновь возвращаемся в ту же область, в которой были раньше. В самом деле, получая то бoльшие, то меньшие числа, мы можем сколь угодно часто возвращаться в некую конечную область. Можно ожидать, что рано или поздно результат вычислений повторится, и, как только это произойдёт, всё дальнейшее предрешено. Образуется замкнутый цикл, из которого уже никогда не выйти. Это объясняется тем, что выбор каждого следующего шага происходит по вполне определённому правилу.
К рассмотренным гипотезам не следует относиться слишком серьёзно: они не могут быть все справедливыми.
Делая эти оговорки, должен тем не менее отметить, что все три гипотезы считаю в высшей степени правдоподобными. Взвешивая каждую из них, я думаю, что не может быть сомнений в её справедливости, и в то же время другие гипотезы мне кажутся не менее убедительными. Что же по этому поводу говорит математический эксперимент?
Начнём вычисления с 1. Это - нечётное число, поэтому, следуя условиям задачи, умножим его
Из всех натуральных чисел единица занимает особое положение: это первое число и наименьшее. Таким образом, результат, полученный для
После исследования первых четырёх натуральных чисел вроде бы выявилась определённая тенденция, но всё же оснований для окончательного вывода нет. В проведённых вычислениях нас больше всего интересуют две величины: максимальное из полученных значений N и длина пути, под которой будем понимать общее число итераций, необходимое для
Снова вернёмся к последовательности, которая порождается начальным
Но если вычисления продолжить, метод <три шага вперёд и два назад> приводит к осциллирующей кривой с постоянно возрастающей амплитудой. Новыми пиками будут 142, 214, 322
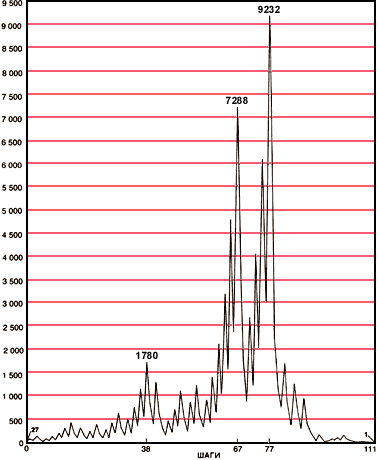
Последовательность значений
Подобные вычисления проводились с огромным набором целых чисел. Сотрудник Токийского университета Набуо Йонеда исследовал все целые числа
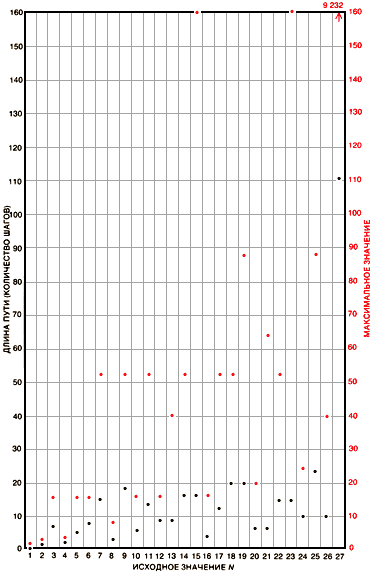
Последовательный перечень самых длинных путей для N от 1 до 100 000 |
Последовательный перечень максимумов для N от 1 до 100 000 |
История проблемы
Лагариас ссылается примерно на 20 научных статей по проблеме
Группой исследователей из Лаборатории искусственного интеллекта Массачусетского технологического института в начале
Постоянно кочуя, задача обрастала множеством имён. Название <проблема
На языке высокого уровня, скажем на Бейсике, можно написать программу для вычисления
IF N MOD 2 = 0 THEN N = N/2 ELSE N = 3*N + 1
Первой здесь записана операция, которую люди (но не машина) выполняют, не прибегая к явным вычислениям: определение чётности (или нечётности) числа N. Компьютер пользуется для этого операцией сравнения по
Такая программа на Бейсике вполне сносно справляется с порождением
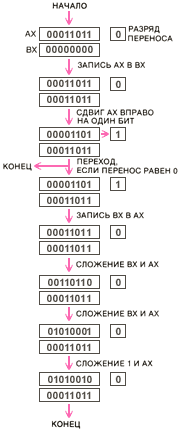
Алгоритм получения
Приблизительное представление о такой программе на языке машины даёт рисунок справа. Предполагается, что исходное значение N первоначально находится в
На первом шаге исходное число в двоичном коде переписывается в другой регистр, обозначенный на
Если N чётное, то вычисления на этом этапе закончены. В
Из рисунка видно, что регистры имеют 8 разрядов и, следовательно, в них нельзя поместить число больше
Алгоритм получения одного значения N - всего лишь фрагмент рабочей программы. В ней, кроме того, должна быть предусмотрена возможность ввода в машину значений и вывода результатов. Реальные же программы для исследования поведения
Разновидности формулы 3N+1, в которых используются другие коэффициенты и постоянные, также плохо поддаются исследованию. У. Госпер и Р. Шоппель, когда они ещё входили в группу HAKMEM, исследовали проблему
Программу, позволяющую лишь выявить числа, которые не попадают в цикл
После всего, что было сказано, по-видимому, нет смысла продолжать поиски числа, которое вело бы себя
Возможно, самые интригующие свойства таких чисел - это выраженный характер распределения максимальных значений и длин пути. Если такое небольшое число, как 27, удерживается <в подвешенном состоянии> в течение 111 шагов и достигает максимума 9232, то можно было бы ожидать, что длина пути и максимальные значения растут так же быстро, как
Среди первой сотни целых чисел самый длинный путь равен 118 шагам
Легко видеть, что максимальные значения, получаемые при вычислении чисел-градин, неизменно чётные. Можно также доказать, что лишь нечётное N способно установить новый рекорд максимального значения (за исключением
Полученная на ЭВМ распечатка длин пути и максимумов для некоторой области целых чисел представляет собой удручающую смесь закономерности и беспорядка. Последовательность безусловно не случайна, но ей не удаётся дать никакого толкования. Например, некоторые максимальные значения повторяются чаще, чем другие, причём появление некоторых максимумов настолько часто, что их нельзя описать
Распределение длины пути столь же хаотично. Можно породить любую из возможных длин пути (последовательностью точных степеней двойки), но и в этом случае некоторые числа будут появляться чаще других. Кроме того, и длины пути, и максимумы проявляют чёткую тенденцию к группированию в кластеры. Ф. Грюнберг из Калифорнийского университета в Нотридже в 1976 году опубликовал перечень таких кластеров. Самый обширный из них представлял собой цепочку из 52 целых чисел, которые проходили одинаково длинный путь. Возникает вопрос: могут ли одинаковые максимумы и одинаковые длины пути достигаться двумя последовательными числами? Ответ на этот вопрос можно дать в алгебраической форме, но если читатель предпочитает демонстрацию на примерах с числами, ему следует рассмотреть последовательности для всех N от 386
Один из подходов, позволяющих пролить свет на задачу о градинах, состоит в обратной её постановке. Предположим, что все положительные целые числа действительно обязательно попадут в цикл
Этот метод прекрасно бы подошёл для получения общего решения задачи о градинах, если бы только его можно было довести до конца. Оказывается, процедура не столь прямолинейна, как кажется. Обычная функция преобразования градин однозначна: у любого значения N в любой точке вычислений только один преемник. Если, например,
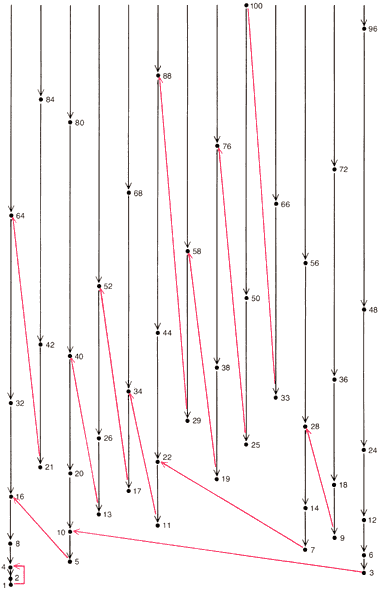
Дерево, порождённое
Такого рода разветвляющуюся систему можно проследить только до определённого уровня. Движемся по отдельной ветви до некоторого наперёд заданного предела и затем переключаем внимание на другую ветвь. При пределе 100 надо будет изучить 13 ветвей, причём в этой числовой системе ручейков и протоков между собой связаны
Хомячковый рай. Уйти и потеряться:
Статистические методы с интенсивным использованием ЭВМ

| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 7 · ИЮЛЬ 1983 · С. 63-74 |
Перси Диаконис, Бредли Эфрон
Эти методы исключают необходимость делать принятые в статистике допущения относительно распределения данных, но сопряжены с колоссальным объемом вычислений. Бутстрэп - один из таких методов. Благодаря ему удалось пересмотреть прежние оценки надежности научных выводов
БОЛЬШИНСТВО статистических методов, широко используемых в настоящее время, известно давно. В основном они были разработаны в период с 1800 по 1930 г., когда вычисления были дорогостоящим и малопроизводительным процессом. Теперь вычисления стоят крайне дешево, а их скорость по сравнению с прошлым возросла в миллионы раз. В последние несколько лет наблюдается резкий подъем в развитии математической статистики: с появлением быстродействующих ЭВМ в этой области возникли новые идеи и методы, реализация которых связана с колоссальным объемом вычислений. Порой необходимо произвести миллион арифметических операций для анализа данных из 15 точек. Столь высокая интенсивность вычислений позволяет освободиться от двух ограничений, изначально господствовавших в математической статистике: от допущения, что плотность распределения данных подчиняется нормальному закону и хорошо описывается колоколообразной кривой, и от необходимости ограничиваться лишь теми статистическими мерами, теоретические свойства которых можно выразить аналитически.
Эти достижения имеют непосредственное отношение к развитию науки в целом, потому что математическая статистика призвана помогать науке в определении истинных значений измеряемых величин. Предположим, что 15 измерений некой величины дали 15 умеренно отличающихся значений. Какое из них послужит самой лучшей оценкой истинного значения? Статистические методы способны дать ответ на этот вопрос и даже выразить количественно надежность такой оценки. Поскольку наблюдения, полученные эмпирическим путем, почти всегда в той или иной мере ошибочны, заключения на основании этих наблюдений должны, как правило, опираться на статистические меры истинности. По-видимому, любое усовершенствование, приводящее к повышению достоверности или степени универсальности выводов, основанных на статистических данных, имеет широкие последствия.
ДЛЯ ТОГО чтобы по достоинству оценить преимущества новых методов, сравним их со старыми. Прежде всего в старых методах, перед тем как приступить к статистическому анализу данных, нужно было, вообще говоря, сделать некоторые малоправдоподобные допущения. Обычно допускается, что статистические данные распределены по нормальному закону, или, как говорят, имеют гауссово (названное так по имени немецкого математика Карла Фридриха Гаусса) распределение, которое можно описать колоколообразной кривой. Использование гауссова распределения означало, что случайные колебания, или ошибки, полученные при определении значений некой величины эмпирическим путем, располагаются симметрично относительно ее истинного значения. Кроме того, чем больше расхождение между истинным и наблюдаемым значением, тем менее правдоподобно это наблюдение. Практика показала, что теория гауссовых распределений дает вполне удовлетворительные результаты, даже если данные не совсем подчиняются нормальному распределению. Это позволило статистикам, обходясь без вычислений, давать достаточно надежные прогнозы. Если же статистические методы применялись к данным, которые не удовлетворяли предположению о гауссовости распределения, то результаты, разумеется, получались совершенно ненадежными. Методами, основанными на интенсивном использовании компьютера, можно решать большинство задач, не вводя предположения о нормальном распределении данных.
Тот факт, что нам удалось избавиться от оков предположения о гауссовости, - безусловно, знаменательная веха в развитии статистики. Но есть еще одно преимущество новых методов, которое дает еще большую свободу. Прежде арифметические операции выполнялись вручную или на настольном калькуляторе. Если формулы, по которым проводились такие вычисления, имели компактное аналитическое выражение, то работа значительно упрощалась. Поэтому в математической статистике появилась тенденция рассматривать лишь несколько характеристик статистической выборки: среднее значение, стандартное отклонение и коэффициент корреляции (поскольку с ними легко оперировать аналитически). Многие другие характеристики, хотя и представляли интерес для статистиков, оказались вне пределов досягаемости для аналитического подхода. Новые методы, опирающиеся на возможности ЭВМ, позволяют исследовать такие характеристики численно, несмотря на то, что их строгий анализ в настоящее время еще неосуществим. Таким образом, эти методы, расширив поле статистических средств, избавили статистиков от необходимости решать более сложные теоретические проблемы.
ДЛЯ ТОГО чтобы проиллюстрировать, как применять компьютер при статистических выводах, остановимся на задаче, данные которой содержат всего 15 точек. Обратимся к методу, разработанному одним из авторов (Эфроном) в 1977 г. и названному бутстрэпом. Идея метода чрезвычайно проста, но он так сильно зависит от возможностей ЭВМ, что каких-нибудь 30 лет назад был бы абсолютно немыслим.
Рассмотрим группу из 15 юридических факультетов, для только что скомплектованных первых курсов которых измеряются две общие характеристики: среднее значение из средних оценок (СО) первокурсников при поступлении и среднее значение баллов, набранных ими на вступительном тестировании юридического профиля (ТЮП). Казалось бы естественным предположить, что эти две меры, грубо говоря, пропорциональны друг другу: первый курс с высокой СО будет иметь тенденцию к высокому среднему баллу ТЮП. Маловероятно, однако, что эта пропорциональность будет строго соблюдаться: первокурсники одного-двух факультетов могут иметь высокое среднее значение СО, но низкий средний балл ТЮП, тогда как на других факультетах может наблюдаться прямо противоположная картина. Статистиков прежде всего интересует, насколько отношение между этими двумя мерами близко к пропорциональной зависимости. Более того, статистиков должно интересовать, насколько точно по тем данным, которыми мы располагаем, можно провести экстраполяцию на остальные юридические факультеты. Короче говоря, как убедиться в том, что выборка 15 юридических факультетов дает точную картину для всей совокупности юридических факультетов в целом?
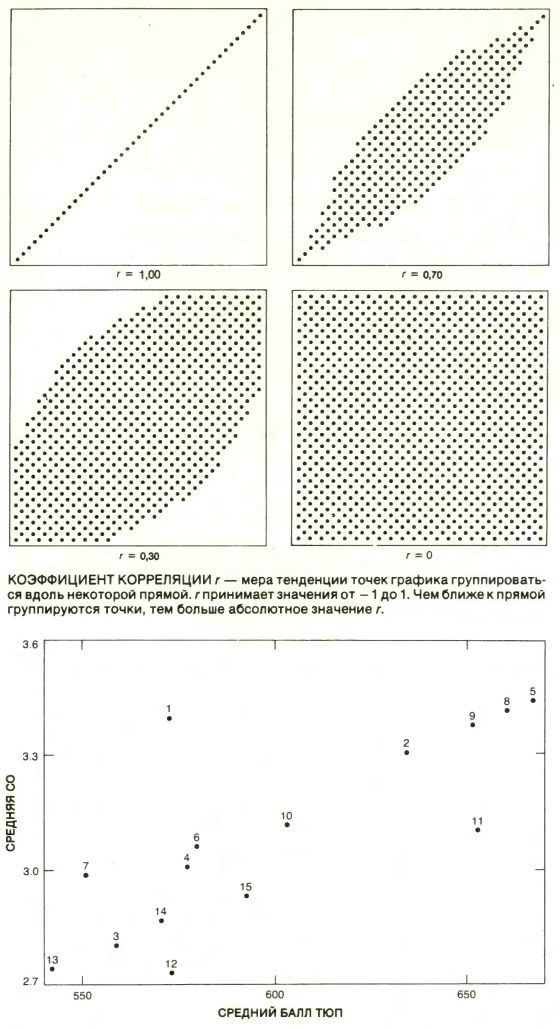
Стандартной мерой близости отношения случайных величин СО и ТЮП к пропорциональной зависимости служит коэффициент корреляции; его обычно обозначают г. Предположим, что данные для юридических факультетов нанесены на график, вертикальная ось которого соответствует СО, а горизонтальная - ТЮП. Коэффициент корреляции позволяет оценить, насколько тесно точки такого графика группируются вдоль прямой. Значение r равно 0, если точки рассеяны случайным образом; чем ближе приближается значение r к 1 или к -1, тем теснее группируются точки вдоль прямой с положительным или отрицательным наклоном. (Прямая имеет положительный наклон, если она направлена вправо вверх, и отрицательный - если вправо вниз.) Корреляция между температурой по Фаренгейту и температурой по Цельсию, например, равна единице, поскольку эти величины строго пропорциональны друг другу. Корреляция между весом отцов и весом их сыновей составляет около 0,5. У полных отцов чаще бывают полные сыновья, но это соответствие не строгое. Корреляция между количеством ежедневно выкуриваемых сигарет и ожидаемой продолжительностью жизни должна быть, очевидно, отрицательной: чем больше ежедневное потребление сигарет, тем короче жизнь.
К0РРЕЛЯЦИЯ между показателями СО и ТЮП, полученными для первых курсов 15 юридических факультетов, оказалась равной 0,776. Иначе говоря, между этими величинами наблюдалась сильная корреляция, а точки графика, построенного в соответствующей координатной плоскости, весьма тесно группировались вдоль прямой с положительным наклоном. Значение r было определено при помощи обычной математической процедуры, которая заняла около пяти минут на настольном калькуляторе. Как именно проводились вычисления - не существенно, достаточно знать, что при помощи этой процедуры можно найти верное значение r для любого набора данных.
Есть ли у нас, однако, основания верить, что истинное значение r для всех юридических факультетов будет хорошо совпадать с 0,776? Ведь в конце концов эта выборка юридических факультетов могла оказаться абсолютно нетипичной. Закон больших чисел дает полную гарантию того, что в случае выборок большого объема статистическая оценка r, вычисленная по такой выборке, с большой вероятностью совпадет с истинным значением r для всей совокупности. Но выборку, содержащую лишь 15 юридических факультетов, большой не назовешь. Следовательно, нам нужна некая мера, при помощи которой можно было бы оценить статистическую достоверность значения r, полученного по данной выборке (в нашем случае равного 0,776). Метод бутстрэпа как раз и дает нам такую меру.
Для того чтобы понять, что означает статистическая достоверность некой оценки, скажем r, предположим, что у нас имеются данные по другим множествам (по другим группам из 15 юридических факультетов), отличающимся от выбранного ранее. Для каждого такого множества можно вычислить значение r и, следовательно, определить количество тех r, которые отличаются друг от друга на определенную величину. Если, например, 99% значений r, вычисленных для этих гипотетических выборок, оказались в интервале между 0,775 и 0,777, то можно считать, что достоверность оценки 0,776 велика. Если же значения r равномерно распределились от -1 до 1, то полученное по первоначальной выборке значение r не будет статистически достоверным, и поэтому оно бесполезно. Иными словами, статистическая достоверность оцененного значения r зависит от ширины интервала, в который заключено это значение. Сам интервал отвечает определенному проценту всех выборок. К сожалению, мы, как правило, не располагаем данными для вычисления r по многим различным выборкам. Таким образом, поскольку пример с юридическими факультетами предназначался для того, чтобы продемонстрировать условия, реально существующие в статистической практике, мы временно будем предполагать, что нам доступны лишь те данные, которые касаются первоначально выбранных 15 факультетов. В самом деле, если бы мы располагали большим количеством данных, то могли бы получить более точную оценку, чем 0,776.
ПРОЦЕДУРА бутстрэпа позволяет произвести оценку статистической достоверности значения r по данным единственной выборки. Идея состоит в имитации процесса получения многих выборок такого же объема, как и исходная выборка (в данном случае 15), чтобы определить, с какой вероятностью значения их коэффициентов корреляции попадают в тот или иной интервал. Эти выборки генерируются из данных первоначальной (исходной) выборки. Название бутстрэп заимствовано из старого идиоматического выражения pulling yourself up by your own bootstraps* и содержит в себе тот смысл, что, располагая лишь одной выборкой, мы можем генерировать необходимое число других выборок, адекватных тем, которые в реальных условиях можно было бы получить случайным образом.
Выборки бутстрэпа генерируются следующим образом. Из данных по первому факультету получают колоссальное количество копий, скажем миллиард; то же самое проделывается с данными по остальным 14 факультетам. Затем 15 миллиардов копий тщательно перемешивают. Теперь выборки, состоящие из 15 наблюдений, выбираются случайным образом и для каждой выборки подсчитывается коэффициент корреляции. На вычислительной машине получение копий, перемешивание и выбор новых данных выполняются при помощи одной процедуры, которая значительно быстрее описанной выше, но эквивалентна ей с математической точки зрения: компьютер приписывает номер каждому юридическому факультету и затем генерирует выборки в соответствии с теми номерами, которые выдает случайное число.
Полученные таким образом выборки называются выборками бутстрэпа. С распределением коэффициентов корреляции для выборок бутстрэпа можно обращаться так же, как если бы это было распределение для реальных выборок: оно дает оценку статистической достоверности значения r, вычисленного на основании исходной выборки. Из данных по 15 юридическим факультетам, имеющимся в нашем распоряжении, мы получили 1000 выборок бутстрэпа. Для 680 из них, т.е. для 68%, коэффициент корреляции оказался в интервале между 0,654 и 0,908. Ширина 0,254 этого интервала и служит мерой бутстрэпа достоверности значения r для данной выборки. Половина ширины интервала (0,127) интерпретируется как оценка среднего значения, на которое наблюдаемое значение r, полученное по случайной выборке объема 15, отличается от истинного значения r.
Важно отметить, что статистическую достоверность нельзя определять просто как достоверность отдельной оценки, например 0,776, т.е. как разность между оценкой и истинным значением r. В реальной задаче эта разность никогда не известна: если бы она была известна, то и задачи бы не было, потому что иначе достаточно вычесть разность из оценки и получить точное значение. Вместо этого статистическая достоверность измеряется, как было указано, средним значением отклонения оценки от истинного значения.
Если результаты по распределениям бутстрэпа использовать в качестве меры статистической достоверности первоначальной оценки, то станет понятно, что оценка 0,776 грубая, но не бесполезная. Истинный коэффициент корреляции, т.е. значение r для совокупности юридических факультетов в целом, мог бы быть между 0,6 и 0,9, но это заведомо не нуль. В нашей теоретической работе показано, что мера бутстрэпа статистической достоверности существенно зависит от разнообразия ситуаций.
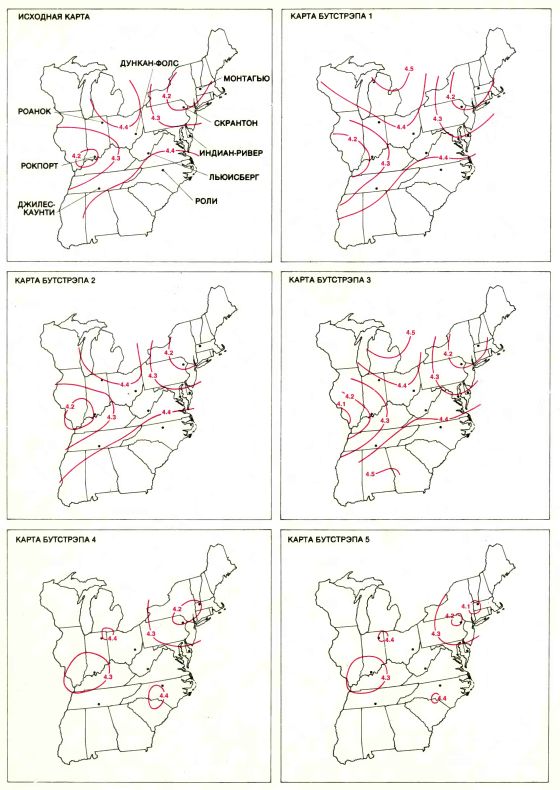
БОЛЬШАЯ ИЗМЕНЧИВОСТЬ изолиний на карте была обнаружена благодаря статистическому методу бутстрэпа. Метод требует громадного объема вычислений, которые можно выполнить только на ЭВМ. Карта вверху слева была получена по данным 2000 измерений кислотности (или значений рН) осадков, полученным на девяти метеорологических станциях за два года. Положение изолиний при некоторых допущениях можно считать оптимальным. Тем не менее, эти 2000 точек подвержены значительной случайной изменчивости: изолинии, полученные по другой выборке, содержащей 2000 измерений, для того же региона и за такой же промежуток времени, могут выглядеть иначе. Бутстрэп, изобретенный одним из авторов статьи (Эфроном), способен по единственному множеству из 2000 данных оценивать величину изменчивости изолиний, как если бы для сравнения имелся ряд множеств из 2000 данных. Результаты пяти расчетов методом бутстрэпа с использованием ЭВМ, проведенные Б. Эйноном и П. Свитцером из Станфордского университета, приведены на остальных пяти картах. Изменчивость изолиний показывает, что исходную карту следует интерпретировать весьма осторожно: коридоры низкой кислотности на исходной карте могут на других картах превратиться в островки.
ДВЕ МЕРЫ потенциальной пригодности к обучению студентов первых курсов 15 юридических факультетов. Точки графика соответствуют усредненным значениям средних оценок (СО) при поступлении и баллов при тестировании по юридическому профилю (ТЮП). Видно, что для данной выборки эти меры имеют тенденцию к пропорциональной зависимости: r = 0,776. Нужно определить, насколько точно значение 0,776 приближается к истинному значению r для всех юридических факультетов университетов США, т.е. насколько наблюдаемое значение r по случайной выборке в среднем отличается от истинного.
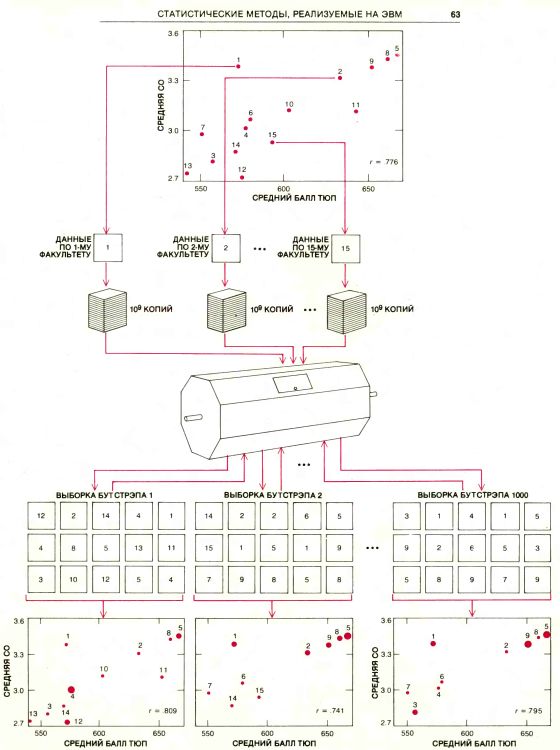
МЕТОД БУТСТРЭПА применили к данным по 15 юридическим факультетам (см. предыдущий рисунок), чтобы убедиться в достоверности r, вычисленного по этой выборке. Данные по каждому факультету размножили до миллиарда экземпляров, и все 15 миллиардов перемешали. Выбирая случайным образом 15 точек из 15 миллиардов, получили искусственные выборки (выборки бутстрэпа). Для каждой из них определили r. Метод прост, но требует большого объем вычислений, невозможных без ЭВМ.
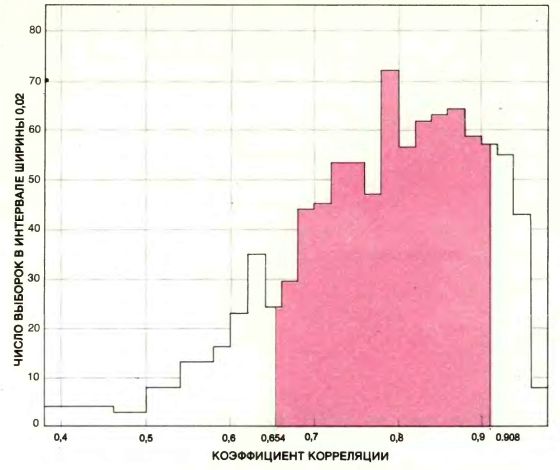
ЧАСТОТНАЯ ГИСТОГРАММА для коэффициента корреляции r, полученная по 1000 выборкам бутстрэпа. Общепринятой мерой достоверности статистической оценки типа r является ширина полосы, находящейся под центральной частью частотной гистограммы. Ее площадь составляет 68% площади, лежащей под всей гистограммой. Центральная полоса для гистограммы бутстрэпа закрашена; ее ширина составляет 0,254. Половина этого интервала 0,127 представляет собой хорошую оценку среднего значения, на которое наблюдаемое значение r отличается от истинного значения r.
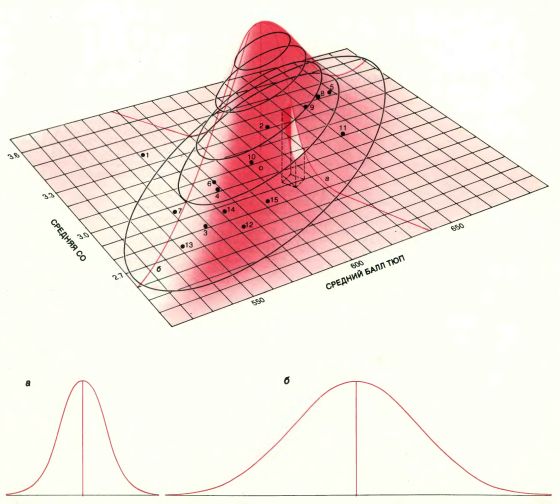
КОЛОКОЛООБРАЗНАЯ ПОВЕРХНОСТЬ была введена в 1915 г. Р. Фишером в его методе оценки по единственной выборке. Он пытался оценить, как сильно отличаются коэффициенты корреляции от выборки к выборке, предполагая, что все данные в выборке получены согласно вероятностям, задаваемым этой колоколообразной поверхностью. Поверхность подгонялась к данным из выборки. В примере с юридическими факультетами самая верхняя точка поверхности должна находиться непосредственно над точкой плоскости, в которой СО и ТЮП имеют их общее среднее значение (открытая окружность). Крутизна и ориентация поверхности относительно плоскости графика зависят от рассеяния точек. Контуры, соответствующие равным высотам, имеют форму эллипсов, а поперечные сечения дают колоколообразные кривые с различной шириной интервала: в нижней части рисунка изображены два поперечных сечения. Метод Фишера можно интерпретировать как получение выборок бутстрэпа из всех таких точек на плоскости графика. Вероятность выбора отдельной точки из некоторой данной области графика равна объему, заключенному между этой областью и колоколообразной поверхностью (объем <дыры>), деленному на весь объем между поверхностью и графиком. Для того чтобы получать выборки бутстрэпа на компьютере, используя лишь дискретные точки исходной выборки, в распределении, задаваемом колоколообразной поверхностью, нет никакой необходимости
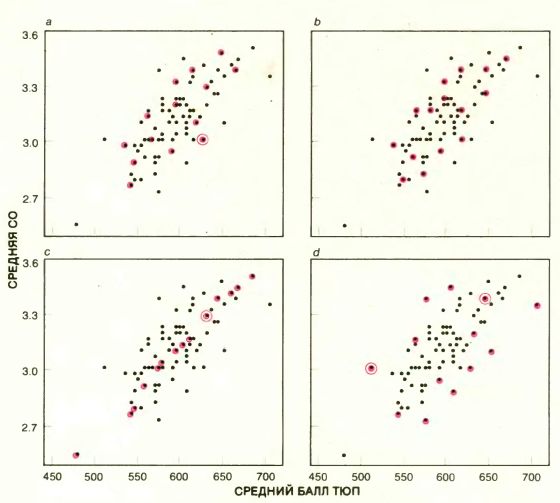
СТАТИСТИЧЕСКАЯ ДОСТОВЕРНОСТЬ значения r, наблюдаемого по случайной выборке, может быть определена корректно, если известно, как изменяется r при большом числе выборок. 15 юридических факультетов, по которым вычислялось значение r, были выбраны случайным образом из полной совокупности 82 юридических факультетов университетов США. Данные на четырех графиках представляют собой средние значения СО и баллов ТЮП для каждого из 82 юридических факультетов. Имеются 8215 способов получать из полной совокупности юридических факультетов выборки объма 15. Четыре такие выборки (с точками, обведенными цветными кружками) указаны на графике. (Каждый факультет может быть выбран более одного раза: соответствующие точки обведены несколькими кружками.) Наблюдаемые значения r для выборок а и b примерно равны истинному значению коэффициента корреляции, полученному по всем 82 факультетам. Значение r для выборки с оказалось значительно выше, а для выборки d - значительно ниже истинного значения. Истинную изменчивость значения r для выборок, содержащих 15 факультетов, можно определить, найдя значение r для многих таких выборок, поскольку у нас в распоряжении имеются данные, значительно превышающие 15 (фактически по всем 82). К сожалению, дополнительные данные зачастую получить невозможно. Бутстрэп способен на основании одной выборки оценить величину изменчивости, которую могли продемонстрировать все выборки.
ТЕПЕРЬ можно признаться, что наше неведение было чистым притворством: в примере с юридическими факультетами достоверность оцениваемого коэффициента корреляции можно проверить непосредственно. В самом деле, мы выбрали этот пример потому, что все данные для среднего значения СО и среднего балла ТЮП по первокурсникам юридических факультетов университетов США за 1973 г. были уже собраны. Коэффициент корреляции между СО и ТЮП для юридических факультетов 82 университетов США оказался равным 0,761. (Следовательно, 0,761 есть то самое истинное значение, о котором неоднократно упоминалось выше, - величина, как, правило, неизвестная.) Но для нас более важно то, что можно определить истинную статистическую достоверность оценки, полученной по первоначальной выборке, потому что можно найти распределение значений r, вычисленных по многим реальным выборкам объема 15. Из 82 юридических факультетов 15 можно выбрать 8215, или около 5x1028, равновероятными случайными способами. В принципе значение r можно было бы вычислять для каждой выборки и, задав равные малые интервалы, построить график числа выборок, для которых значение r попадает внутрь определенного интервала. Полученный при этом график называется частотной гистограммой.
На самом деле можно получить только приближенную частотную гистограмму для выборок объема 15 из 82 юридических факультетов: если бы компьютер с быстродействием 1 млрд. операций в 1 с вычислял значения r для всех 8215 выборок, ему потребовалось бы больше лет, чем прошло со времени сотворения мира. Поэтому r вычисляют для большого, но реально осуществимого числа выборок, например для 1 миллиона.
Было обнаружено, что 68% коэффициентов корреляции, подсчитанных для миллиона выборок, оказались в интервале между 0,606 и 0,876, ширина которого составляет 0,270. Иначе говоря, если 15 юридических факультетов выбраны случайным образом, вероятность того, что коэффициент корреляции попадает в интервал между 0,606 и 0,876, равна 0,68. Заметим, что ширина этого интервала почти совпадает с шириной интервала, полученного для 68% выборок бутстрэпа, хотя в своих крайних точках интервалы различаются больше.
Оказывается, такое совпадение не случайно, и это подтвердили теоретические исследования, проведенные рядом ученых: Р. Бираном, П. Бикелом и Д. Фридманом из Калифорнийского университета в Беркли, а также Сингхом из Ратгерского университета и авторами настоящей статьи из Станфордского университета. Для коэффициента корреляции и для многих других статистических характеристик ширина интервала, соответствующего распределению бутстрэпа, и ширина интервала, соответствующего реальному распределению, как правило, совпадают. (Обычно сравниваются интервалы, в которые попало 68% выборок, потому что для колоколообразной кривой 68% выборок находится по обе стороны от точки, где достигается максимальное значение кривой, на расстоянии, не превышающем стандартного отклонения.)
НА ПЕРВЫЙ взгляд этот теоретический результат кажется- парадоксальным: выходит, что из информации об одной выборке можно получить вполне удовлетворительную аппроксимацию частотной гистограммы коэффициента корреляции для всех реальных выборок того же объема. Значит, статистики открыли нечто вроде статистического аналога голограммы - образа световых волн, застывших на поверхности. Объемный образ, послуживший источником этих волн, может быть во всех подробностях восстановлен по всей поверхности голограммы, но даже если голограмму разбить на фрагменты, то объект можно восстановить по любому фрагменту. Но, оказывается, не всякая выборка подобна фрагменту голограммы: хорошие качества бутстрэпа - это лишь хорошие качества в среднем. Подобно любой иной статистической процедуре, бутстрэп будет вводить нас в заблуждение для небольшого процента возможных выборок.
Предположим, что коэффициент корреляции для выборки, состоящей из данных по 15 юридическим факультетам, оказался примерно равным 1. Иначе говоря, все точки выборки расположились почти точно вдоль прямой. Учитывая, что реальные данные собраны по 82 факультетам, такая ситуация маловероятна, но тем не менее она возможна. В этом случае каждая выборка, полученная процедурой бутстрэпа, должна была бы тоже располагаться вдоль той же прямой, и поэтому все полученные бутстрэпом значения r равнялись бы примерно 1. Ширина интервала, соответствующего 68% выборок бутстрэпа, равнялась бы, таким образом, приблизительно нулю. Итак, на основании процедуры бутстрэпа заключаем, что статистическая достоверность оцениваемого значения r будет почти идеальной, тогда как на самом деле она ошибочна.
Бутстрэп не всегда может гарантировать, что статистическая достоверность выборочной оценки соответствует действительности. Единственное, что было доказано, - это то, что бутстрэп большей частью дает хорошую картину достоверности оценки. Всегда существует небольшая доля выборок, для которых бутстрэп не работает, и никто заранее не знает, какие именно это выборки. Указанные ограничения не являются таким уж серьезным недостатком процедуры бутстрэпа, а представляют собой всего лишь переформулировку условий неопределенности, при которых и должен проводиться всякий статистический анализ.
КАКИЕ ЖЕ достоинства имеет бутстрэп? Для того чтобы оценить их в полной мере, полезно описать, как вычислялась достоверность коэффициента корреляции (и большинства других статистических характеристик) в те времена, когда компьютеры не были столь широкодоступны. Эту процедуру можно описать в терминах бутстрэпа, хотя до изобретения компьютера статистики не пользовались такими терминами в своих работах. Английский статистик Р. Фишер в 1915 г. теоретически определил достоверность коэффициента корреляции r. Он полагал, что значения двух случайных величин (в нашем примере это средние значения СО и ТЮП) были получены случайным образом из нормального распределения, плотность которого представлена колоколообразной поверхностью. Это двумерный аналог одномерной колоколообразной кривой. Имеются семейства таких поверхностей, форму и ориентацию которых можно выбрать так, чтобы они служили подгонкой для имеющегося множества данных. Эта поверхность подгоняется к данным выборок из юридических факультетов таким образом, чтобы вершина колокола расположилась прямо над точкой графика, в которой величины СО и ТЮП имеют их общее среднее значение. Крутизна спуска поверхности к графику зависит от того, как широко рассеяны точки (см. рисунок на с. 8).
Колоколообразная поверхность интерпретируется как плотность распределения вероятностей, точно так же как график значений r для выборок юридических факультетов представляет собой частотную гистограмму. Вероятность выбрать точку на графике СО и ТЮП из некоторой области равна объему между колоколообразной поверхностью и этой областью, деленному на весь объем между поверхностью и графиком. Теперь Фишер мог бы приступить к построению гистограммы для значений r методом бутстрэпа, исходя из колоколообразной плотности распределения. В самом деле, большое количество выборок, состоящих из 15 точек, выбиралось на графике в соответствии с вероятностью, задаваемой их расположением под колоколообразной поверхностью. Значение r вычислялось для каждой выборки и строилась гистограмма значений г. Согласно методу Фишера, ширина интервала, в который попадает 68% значений r, равна 0,226, что неплохо совпадает с истинным значением 0,270, но оценка 0,254 бутстрэпа совпадает с ним лучше.
Благодаря предположению, что данные в выборке получены из нормального распределения, весь объем вычислений в методе Фишера можно выполнить аналитически. Такое предположение - недостаток метода, поскольку оно не всегда выполняется. В нашем примере с юридическими факультетами дело именно так и обстоит. Кроме того, даже если такое предположение справедливо, нет простого способа проверить это: в большинстве ситуаций выборки, которые должны быть проверены на соответствие с формой поверхности, бывают значительно большего объема, возможно с несколькими сотнями данных.
30 лет назад вычисления по методу бутстрэпа - не будь упрощающих предположений относительно распределения вероятностей - были бы совершенно невыполнимы. Как уже говорилось, вычисление одного коэффициента корреляции занимает около пяти минут на настольном калькуляторе, а на получение частотной гистограммы для выборок бутстрэпа потребуется от 50 до 1000 таких вычислений.
Сегодня вычисление одного значения r на компьютере средних возможностей длится 0,0001 с; при такой скорости бутстрэп становится доступным для повседневного применения. Если этим методом требуется получить 1000 выборок, все вычисления, необходимые для оценки ширины интервала, в который попадает 68% выборок, займут меньше секунды и обойдутся самое большее в 1 долл. Предполагается, что быстродействие компьютера - 100 тыс. арифметических операций в секунду. На более тщательный анализ бутстрэпом, при котором выдается более подробная информация относительно достоверности r, потребуется около 1 млн. арифметических операций.
Использование метода бутстрэпа не ограничивается анализом изменчивости статистических характеристик вроде коэффициента корреляции - эти величины имеют простое математическое выражение. Он применялся и во многих задачах, в которых изменчивость интересующей нас статистической характеристики нельзя было получить аналитически. Рассмотрим семейство статистических данных, называемых главными компонентами, которое в 1933 г. ввел X. Хоттелинг из Колумбийского университета. Главные компоненты были придуманы для решения задачи типа приводимой ниже, взятой из учебника К. Мардиа и Дж. Кента из Лидского университета и Дж. Биббииз Открытого университета.
Среди 88 учащихся колледжа проведены два тестирования без разрешения пользоваться учебниками и три тестирования - с разрешением. Предположим, для того чтобы вывести определенный балл каждому ученику, мы хотим найти взвешенное среднее по результатам пяти тестов, которое даст наибольшую дифференциацию знаний учащихся. (Для того чтобы сделать отношения, а не только разности по всем баллам настолько различными, насколько это возможно, веса должны быть нормированы таким образом, чтобы их сумма квадратов равнялась 1). Одно из множеств весов возникает, если рассматривается только количество баллов по последнему тесту: тогда нужно назначить веса 0,0,0,0,1. Если все учащиеся имеют высокие баллы по этому тесту, общий балл, полученный суммированием с такими весами, не даст эффективной дифференциации студентов. Другой общий балл выводится, если каждому тесту приписать один и тот же вес. Значением этого весового коэффициента будет 1/
Первую главную компоненту невозможно представить в аналитическом виде - ее следует получить численно. Расчеты, проведенные для группы из 88 учащихся, показали, что веса первой главной компоненты оказались приблизительно равны друг другу. Следовательно, мы будем иметь наибольшую дифференциацию учеников, если возьмем средний балл по пяти тестам.
Второй главной компонентой служит множество весов, удовлетворяющее некоему математическому ограничению о независимости, что дает нам вторую наибольшую дифференциацию учащихся. Вторая главная компонента, вычисленная для группы из 88 учеников, выявила то обстоятельство, что веса для средних баллов по тестам, в которых разрешалось пользоваться учебником, отличаются от весов по тестам, в которых это запрещалось. Главные компоненты предлагают полезные и неожиданные интерпретации средних баллов учеников. Заслуживают ли доверия эти интерпретации? Если им доверять можно, то нужно стараться определить, сколь сильно отличаются значения этих двух главных компонент для выборок, полученных случайным образом.
Вот уже 50 лет умы статистиков занимает проблема получения количественного выражения для изменчивости главных компонент применительно к выборкам данного размера. Если данные удовлетворяют нормальному распределению, то можно дать частичный ответ на вопросы, связанные с построением гистограммы для первой главной компоненты. Что касается второй компоненты и других компонент более высоких порядков, то здесь известно немного. Применение же метода бутстрэпа на ЭВМ может быстро дать оценку изменчивости для любой главной компоненты, даже без введения ограничения о гауссовости распределения.
В принципе анализ методом бутстрэпа здесь проводится так же, как и для коэффициента корреляции. Каждое множество баллов учащихся по пяти тестам было размножено в большом количестве (т.е. все пять полученных баллов записывались на одинаковых листах бумаги), и полученные копии были тщательно перетасованы. Из них случайным образом выбирается 88 экземпляров и вычисляется главная компонента. Этот процесс многократно повторяется, и для каждой главной компоненты строится частотная гистограмма.
Результаты показывают, что веса, связанные с первой главной компонентой, очень устойчивы: они отличаются только во вторых десятичных знаках. Веса, связанные со второй главной компонентой, менее устойчивы, но в некотором структурном смысле. Вспомним, что вторая главная компонента интерпретировалась как разность между средним баллом по тестам без учебника и средним баллом по тестам с учебником. Такая интерпретация подтвердилась анализом по методу бутстрэпа, но веса, задаваемые тестом с учебником, оказались самыми разнообразными. Распределение для главных компонент, полученное бутстрэпом, даёт хорошую оценку истинного распределения главных компонент для выборок объема 88. На мощных компьютерах получение сотни распределений бутстрэпа занимает 2 с.
НЕ КАЖДАЯ статистическая оценка выражается каким-то числом. На девяти метеорологических станциях восточных и среднезападных штатов США регистрировался уровень рН (кислотности) всех осадков с сентября 1978 г. до августа 1980 г. (Значение pН, меньшее 7, означает кислую среду; чем ниже значение рН, тем выше кислотность.) За два года было получено 2000 значений рН. Для представления этих данных Б. Эйнон и П. Свитцер из Станфордского университета изготовили карты изолиний рН этого региона: вдоль изолиний значение pН постоянно. Такие карты получают по данным при помощи строгой математической процедуры, называемой методом Крайга (по имени горного инженера X. Крайга из ЮАР). Хотя карта изолиний точно определяется данными, она представляет собой некую экстраполяцию данных, собранных на 9 метеорологических станциях, на множество точек в пространстве и во времени (фактически на бесконечное их число), которые не были включены в исходную выборку. Можно задаться вопросом: как будут меняться карты изолиний в зависимости от случайных изменений в различных выборках, состоящих из 2000 значений pН?
В этом примере не известны ни истинная карта изолиний, ни истинная изменчивость всех карт, порожденных выборками 2000 значений pН. Обе оценки должны быть получены из единственной исходной карты, если это вообще возможно. Методом бутстрэпа, сохраняя географическое расположение станций, Эйвон и Свитцер из 2000 значений рН исходной выборки получили карты, изображенные на с. 4. Вообще говоря, нет общепринятой меры изменчивости изолиний на карте, аналогичной ширине интервала для гистограмм. Интуитивно, однако, эта изменчивость легко различается. Поэтому исходную карту изолиний следует интерпретировать очень осторожно. Коридоры относительно низкой или относительно высокой кислотности под влиянием случайного <шума> могут сжаться на карте бутстрэпа до островков.
Нередко при статистическом оценивании к имеющимся в нашем распоряжении данным подбирают некоторую заранее заданную линию или модель так, чтобы она по возможности точно совпадала с ними. Простейшими моделями служат прямая, плоскость и ее аналоги более высокой размерности. Рассмотрим 15 точек, представляющие 15 юридических факультетов. Интуитивно понятно, что существует много линий, которые можно провести так, чтобы они отразили ту или иную тенденцию полученных точек. Поэтому разумно заранее оговорить некоторую меру достоверности метода подгонки.
По-видимому, наиболее популярна оценка статистических характеристик методом наименьших квадратов. Метод был изобретен Гауссом и Лагранжем в начале XIX в. для оценки предсказаний в астрономии.
Прямая наименьших квадратов (представляет собой прямую линию, сумма квадратов всех расстояний с которой до имеющихся точек минимальна. Уравнение для прямой наименьших квадратов можно получит непосредственным вычислением. Если к данным применяется метод бутстрэпа, то порождаются фиктивные множества данных, к каждому из которых применяется метод наименьших квадратов для подгонки к ним новой прямой. Флуктуация таких прямых, порожденных бутстрэпом, показывает изменчивость метода наименьших квадратов как статистической оценки для этого множества данных.
Метод наименьших квадратов и его обобщения особенно полезны при решении сложных задач, когда исследователь нуждается в большом количестве разнообразной информации, относящейся к одному явлению. Министерство энергетики США, например, разработало модель Regional Demand Forecasting Model (RDFOR) предсказания спроса по регионам, которая представляет собой попытку предсказать спрос на энергию в 10 регионах США. Предполагается, что спрос на энергию в каждом регионе в данном году зависит неким элементарным образом от пяти переменных: количества дней летом, когда температура превысила 24° С, количества дней зимой, когда температура была ниже 18° С, цен на топливо, условно-чистой продукции обрабатывающей промышленности (мера экономических условий данного региона) и спроса на энергию в предыдущем году.
ЭТИ ПЯТЬ переменных можно представить графиком в пятимерном пространстве, который в сущности аналогичен двумерному графику: каждой точке пятимерного графика соответствует определенная комбинация из пяти переменных. Спрос на энергию в данном году, отвечающий известной комбинации переменных, можно тогда представить высотой, опущенной из некоторой точки шестимерного пространства в соответствующую точку графика в пятимерном пространстве. Представление данных в шестимерном пространстве аналогично представлению зависимости некоторой величины от двух других переменных: высоты, опущенной из точек в трехмерном пространстве на двумерный график. Таким образом, данные спроса на энергию определяют множество высот в шестимерном пространстве.
Метод наименьших квадратов дает способ получения пятимерного аналога плоскости (называемого гиперплоскостью), расположенной как можно ближе ко всем точкам. Поскольку имеется зависимость от спроса на энергию в предыдущие годы, гиперплоскость следует подгонять к переменным обобщенным вариантом метода наименьших квадратов. В обобщенном методе предусматривается минимизация взвешенных сумм ошибок после того, как веса были оценены по данным. В последние годы был разработан усовершенствованный метод оценки достоверности этой процедуры и достоверности даваемых при ее помощи прогнозов.
Фридман и С. Питере из Станфорда применили бутстрэп для изучения общепринятых оценок достоверности этой процедуры. В их подходе предполагалось, что данные тесно примыкают к подходящей гиперплоскости, но не предполагалось, что ошибки между данными и точками на гиперплоскости не зависят друг от друга. Вместо этого допускалось, что отношение ошибок от точки к точке может иметь сложную структуру. Бутстрэп применялся к данным с учетом сохранения тенденции спроса на энергию от года к году. Изменчивость гиперплоскостей, порожденных бутстрэпом, показала, что ранее предполагаемая стандартная ошибка энергетической модели была очень занижена - вдвое или втрое. Таким образом, прогнозы на спрос энергии, полученные на основе модели RDFOR, оказались значительно менее надежными, чем считалось ранее.
ВЫБОРКИ в рассмотренных примерах имели четко определенные статистические свойства. На практике, прежде чем приступать к формальному анализу, данные тщательно проверяют, сортируют, изображают графически, подвергают предварительному неформальному анализу. Оценки, при которых не проводится такой неформальный анализ, не могут дать достоверную картину статистической изменчивости.
Рассмотрим группу из 155 больных острым и хроническим гепатитом, которых наблюдал П. Грегори, сотрудник медицинского факультета Станфордского университета. Из 155 пациентов выжили 122 и умерли 33; о каждом пациенте были собраны данные по 19 показателям, таким, как возраст, пол и результаты стандартных биохимических измерений. Грегори ставил своей целью выяснить, можно ли эти данные свести в модель, позволяющую предсказывать шансы отдельного пациента на выздоровление.
Анализ данных проводился в несколько стадий. Прежде всего были исключены все переменные, кроме четырех самых важных, поскольку статистический опыт нам подсказывает, что было бы неразумно, имея только 155 точек, подгонять модель, зависящую от 19 переменных. Исключение переменных проводилось в два этапа: сначала каждая переменная изучалась по отдельности, после чего были исключены шесть, по-видимому не имеющих отношения к выживанию пациентов. К оставшимся 13 переменным была применена некая стандартная статистическая процедура, после чего их число сократилось до четырех. Остались следующие показатели: самочувствие больного, асцит (наличие жидкости в брюшной полости), содержание билирубина в печени и мнение лечащего врача относительно возможного исхода для больного. По этим переменным строилась подогнанная кривая, по которой можно было предсказать, как относительное число выживших пациентов зависит от значений переменных.
Анализ, состоящий из нескольких стадий, типичен для научной практики. Для того чтобы оценить общую изменчивость всех стадий, Г. Гонг из Университета Карнеги - Меллона провела всю процедуру целиком - от предварительного отбора до окончательной подогнанной кривой - по выборкам бутстрэпа, полученным из исходных 155 точек. Ее результаты оказались неожиданными и весьма информативными. Множество "самых важных" переменных, полученное на первой стадии анализа, уже само оказалось абсолютно ошибочным. Для некоторых выборок бутстрэпа важным был только прогноз лечащего врача относительно исхода, тогда как для других - такие переменные, как пол, возраст, переутомление, содержание альбумина и содержание белка. Не оказалось ни одной переменной, которая бы проявила себя как важная в 60% выборок бутстрэпа.
Хотя подогнанная кривая предназначалась для того, чтобы предсказывать, выживет или нет данный больной, в 16% случаев из 155 обследуемых пациентов классификация оказалась ошибочной. Оценка 16%, однако, тоже слишком занижена, поскольку данные, из которых она получена, использовались и для построения кривой. Анализ на основании выборок бутстрэпа дал улучшенную оценку для вероятности того, что подогнанная кривая будет ошибочно классифицировать данного пациента: оценка оказалась равной 0,20. Если в перспективе методом бутстрэпа можно будет проводить целиком весь процесс анализа данных, то есть надежда когда-нибудь подступиться и к одной чрезвычайно сложной задаче - к связи между математической теорией, лежащей в основе математической статистики, и реальной статистической практикой. Обычно считалось, что предварительно <совать нос> в окончательные результаты бесполезно, и для этого выдвигалось сомнительное основание, что их невозможно исследовать аналитически. Теперь очевидно, что бутстрэп, призвав на помощь компьютер, может начать оценивать пользу такого вмешательства.
БУТСТРЭП, разумеется, не единственный метод, полагающийся на мощь компьютера. Несколько других статистических методов, таких, как <метод складного ножа>, перекрестная проверка достоверности, сбалансированное повторение экспериментов, по сути аналогичны бутстрэпу, но в деталях сильно от него отличаются. В каждой из этих процедур из исходных данных генерируются фиктивные множества и затем оценивается размер реальной изменчивости статистической характеристики по ее изменчивости, полученной по всем фиктивным множествам данных. Друг от друга и от бутстрэпа эти методы отличаются способом получения фиктивных множеств данных.
Первым появился <метод складного ножа>. Его изобрел М. Кенуй в 1949 г., а усовершенствовали в 1950 г. Дж. Тьюки из Принстонского университета и сотрудники фирмы Bell Laboratories. Исследования практической возможности этого метода проводили К. Мэллоуз из фирмы Bell Laboratories, Л. Джекел из Университета в Беркли, Д. Хинкли из Техасского университета в Остине, Р. Миллер из Станфордского университета, У. Шуканы из Южного методического университета и многие другие. Название <складной нож>, придуманное Тьюки, указывает на универсальность этого статистического инструмента.
В методе складного ножа предусматриваются удаление по одному наблюдению из исходной выборки и вычисление заново для каждого из полученных усеченных множеств интересующей нас статистической характеристики. Таким образом, можно описать изменчивость этой статистической характеристики по всем усеченным множествам данных. При оценке точности значения r для данных по 15 юридическим факультетам методом складного ножа проводится 15 новых вычислений r, по одному для каждой возможной выборки объема 14. В методе складного ножа меньше вычислений, чем в бутстрэпе, но это говорит о его меньшей гибкости, а порой и меньшей надежности.
В методе перекрестной проверки достоверности воплощена простая идея. Данные разбиваются пополам и кривые, подогнанные к одной части, одна за другой проверяются на наилучшее совпадение с другой частью данных. В результате перекрестной проверки достоверности получаем надежный показатель того, насколько хорошо подогнанная кривая будет предсказывать значения новых данных. Кстати, разбиение пополам не обязательно, данные с таким же успехом можно разбить в пропорции 90 к 10. Кроме того, нет никаких оснований проводить перекрестную проверку лишь один раз: данные можно разбивать многими способами и в каждом случае брать всевозможные случайные сочетания.
Перекрестная проверка достоверности широко применяется в ситуациях, когда процедура подгонки кривой корректно определена во всех отношениях, за исключением одного очень существенного. Пусть, например, методом наименьших квадратов требуется подогнать к данным многочлен, но его степень, или самый высокий показатель, все еще вызывает сомнения. (Чем выше степень многочлена, тем менее гладкой будет подогнанная кривая.) Если к одной половине данных подгонять многочлены разной степени, то перекрестной проверкой можно выбрать степень многочлена, лучше всего согласующегося со второй половиной данных. С. Гейсер из Университета штата Миннесота, М. Стоун из Лондонского университета и Г. Вазба из Университета штата Висконсин были пионерами в этом направлении.
Вместо разбиения данных пополам случайным образом была разработана более упорядоченная система разбиений. Выбирается такая система разбиений, что в некоторых простых ситуациях, допускающих полный статистический анализ, получились оптимальные результаты. В методе сбалансированного повторения экспериментов, разработанном Ф. Маккарти из Корнеллского университета, дается такое систематическое разбиение данных, при котором оцениваются изменчивость наблюдений и полный набор статистических характеристик. Родственный метод случайных подвыборок, разработанный Дж. Хартиганом из Иельского университета, предназначен для установления в некоторых ситуациях надежных доверительных интервалов.
МЕЖДУ описанными методами существует тесная теоретическая взаимосвязь. Все они, а также ряд других получены из бутстрэпа и объединены одной идеей. Следовательно, мы вправе спросить, как часто бутстрэп будет давать верный результат для определенного класса задач и насколько широк круг задач, к которым его можно применить. На первый вопрос ответить просто. Бутстрэп был испытан на большом количестве задач типа задачи о юридических факультетах, правильный ответ для которых известен. Оценка получилась хорошей, и можно доказать математически, что для аналогичных задач метод также будет пригоден.
Ответ на второй вопрос можно дать лишь на основании уже имеющихся результатов решения множества сложных задач с помощью бутстрэпа. Однако необходимо убедиться, что в этих задачах достоверность оценки, полученной по методу бутстрэпа, столь же высока, как и в более простых задачах. В последних теоретических работах предпринимаются попытки найти такое обоснование и более строго определить точность, обеспечиваемую методом бутстрэпа. Фишер сумел дать на статистическую теорию, которая и пользовала все преимущества, предоставляемые вычислительными средствами 20-х гг. Теперь перед нами стоит задача - осуществить нечто подобно для 80-х гг.
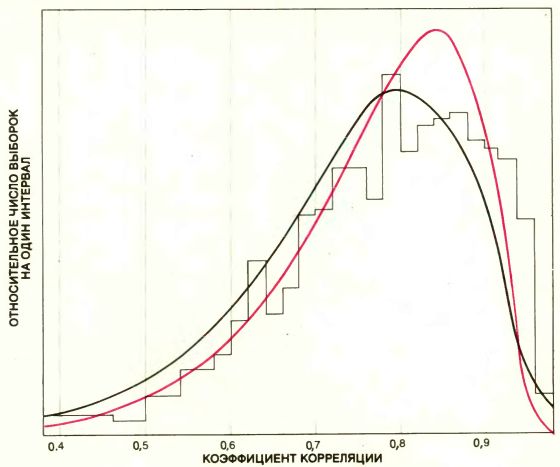
ГИСТОГРАММА БУТСТРЭПА для коэффициента корреляции г (черная линия, напоминающая очертания здания) дает хорошее приближение для истинной плотности распределения коэффициента r (плавная черная кривая). Истинное распределение фактически было получено для миллиона выборок объема 15, взятых случайным образом из 8215 всех возможных выборок из 82 юридических факультетов. Разница между распределением, изображенным здесь, и тем, которое может быть в принципе построено по всем 8215 выборкам, несущественна. Форма распределения бутстрэпа также очень близка к форме того распределения, которое можно оценить согласно вероятностям, задаваемым колоколообразной поверхностью (плавная цветная кривая). Такое хорошее совпадение позволяет полагать, что бутстрэп можно использовать в качестве меры точности, с которой коэффициент корреляции выборки совпадает с коэффициентом корреляции всей совокупности. Хорошее совпадение пиков распределения представляет собой некий артефакт выборки.
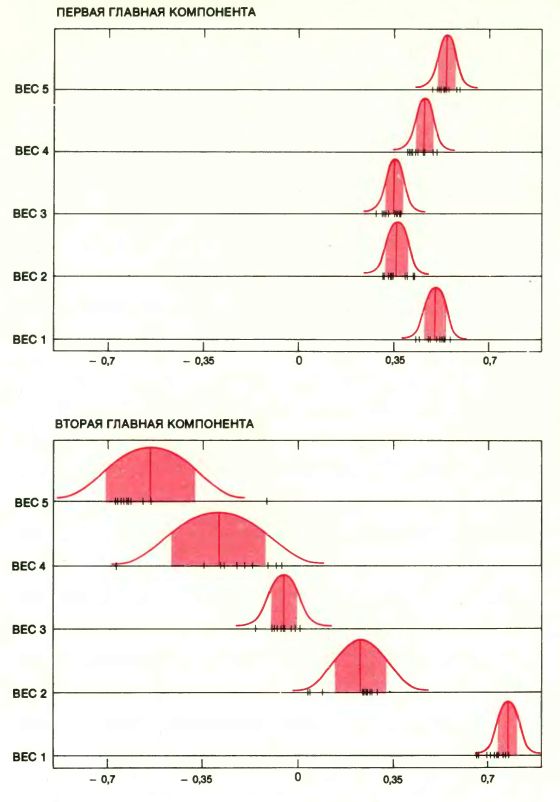
ГЛАВНЫЕ КОМПОНЕНТЫ представляют собой статистические оценки, широко применяемые при подсчете общего балла тестирования. Предположим, что все 88 учащихся подверглись пяти тестам. Для того чтобы вывести общий балл, нужно найти взвешенное среднее баллов по каждому из пяти тестов, которое бы давало самое большое различие среди учеников. Первая главная компонента представляет собой множество весов, дающее решение этой задачи. Вторая главная компонента есть множество весов, подчиняющихся некоему математическому допущению о независимости, и это множество порождает комбинацию баллов, дающую вторую наиболее сильную дифференциацию. Чтобы определить изменчивость двух главных компонент для многих дополнительных выборок объема 88, к единственной выборке был применен бутстрэп. Баллы, полученные каждым учащимся по пяти тестам, были выписаны на листке бумаги, и каждый такой список был многократно повторен. После тщательного тасования всех копий из них случайным образом получались выборки бутстрэпа объема 88. Для каждой выборки были найдены главные компоненты. Черные деления на графиках соответствуют возможным значениям весов для первых 10 выборок; красными вертикальными линиями указаны наблюдаемые значения этих весов. Ширина центральной полосы под малыми колоколо-образными кривыми дает представление об изменчивости весов. Четвертый и пятый весовые коэффициенты второй главной компоненты совершенно неустойчивы.
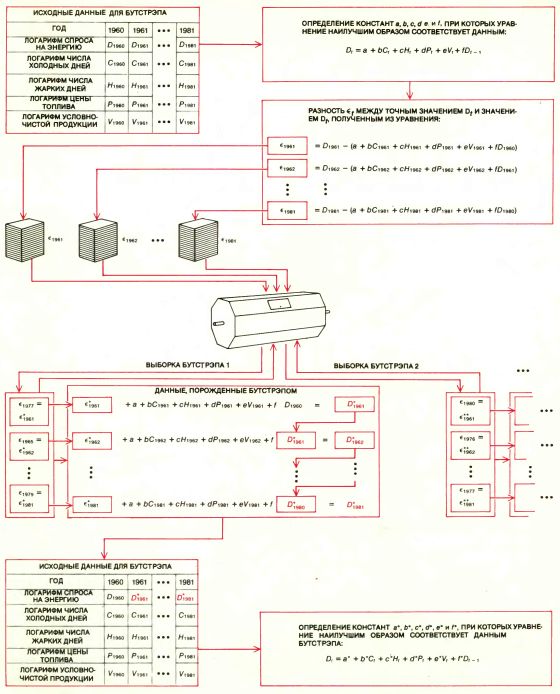
МОДЕЛЬ СПРОСА НА ЭНЕРГИЮ RDFOR (Regional Demand Forecasting Model) была разработана Министерством энергетики США для анализа и предсказания спроса на энергию в 10 регионах страны. К данным по каждому региону была как можно ближе подогнана математическая модель, называемая уравнением регрессии. Предполагалось, что спрос на энергию в текущем году зависит от спроса на энергию в предыдущем году и от нескольких других факторов. Каждая ошибка ?r представляет собой разность между предсказанным значением спроса на энергию в текущем году и наблюдаемым значением. Выборки бутстрэпа, состоящие из ошибок, выбираются случайно, а искусственные данные спроса на энергию порождаются методом, представленным на диаграмме. К данным бутстрэпа затем подгоняются новые уравнения регрессии; изменчивость уравнений регрессии, порожденных бутстрэпом, дает оценку ожидаемой точности модели предсказания спроса на энергию. Анализ с помощью бутстрэпа, проведенный Д. Фридманом из Калифорнийского университета в Беркли и С. Питерсом из Станфордского университета, показал, что изменчивость уравнений регрессии в два-три раза выше, чем предполагалось прежде.

ДАННЫЕ МЕДИЦИНСКОГО ОБСЛЕДОВАНИЯ семи из 155 пациентов с острым или хроническим гепатитом представлены в виде 19 показателей для каждого больного, по которым в совокупности можно предсказать, умрет пациент или оправится от болезни. (Звездочка означает, что информация отсутствует.) До построения формальной модели данные внимательно изучаются. Это делается с целью исключить из рассмотрения все малозначащие показатели, кроме четырех-пяти самых важных. П. Грегори, сотрудник медицинского факультета Станфордского университета, при анализе исключил все переменные, кроме недомогания больного, наличия асцита (жидкости в брюшной полости), содержания билирубина и мнения врача о возможном исходе. На основании этих четырех переменных Грегори разработал модель, которая в 84% случаев давала правильный прогноз.

ПЕРЕМЕННЫЕ, ПРИЗНАННЫЕ ВАЖНЫМИ при неформальном анализе, предшествующем построению формальной статистической модели, оказались самыми разнообразными. Применение бутстрэпа для моделирования формального и неформального аспектов статистического анализа осуществила Г. Гонг из Университета Карнеги - Меллона. Копирование 19 переменных, связанных с каждым пациентом, было запрограммировано на ЭВМ. Множества данных были тщательно перемешаны, и затем из них случайным образом делались выборки 155 множеств данных. Затем к каждой выборке бутстрэпа применялась формальная и неформальная техника анализа данных, точно так же, как это делалось для исходной выборки. Для 10 из 500 выборок, полученных бутстрэпом, приведены показатели, признанные для них важными. Не нашлось ни одной переменной, из четырех первоначально отобранных, которая была бы признана важной в 60% случаев. Следовательно, не стоит слишком серьезно относиться к переменным, признанным важными при неформальном анализе.
Хомячковый рай. Уйти и потеряться:
'Я мыслю - следовательно, дискредитирую'