Нетранзитивные кости Эфрона
Использование нетранзитивных костей влияет на результат игры со следующими правилами:
Первый игрок выбирает игровую кость из набора.
Второй игрок выбирает одну из костей, которые остались в наборе после выбора первого игрока.
Оба игрока бросают свои кости; выигрывает игрок, у которого выпало большее число.
При использовании транзитивных костей преимущество в игре имеет первый игрок, который может выбрать кость, результат броска которой с вероятностью минимум 50 % будет больше результата броска любой другой кости из набора. В случае же использования набора нетранзитивных костей преимущество получает второй игрок, который, независимо от выбора первого игрока, может выбрать из оставшихся костей такую, бросание которой с вероятностью более 50% превысит результат первого игрока.
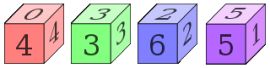
Кости Эфрона — набор из четырёх нетранзитивных костей, изобретенный Брэдли Эфроном.
Четыре кости $A$, $B$, $C$, $D$ имеют на своих гранях следующие числа:
| $A:$ | 4, | 4, | 4, | 4, | 0, | 0 |
| $B:$ | 3, | 3, | 3, | 3, | 3, | 3 |
| $C:$ | 6, | 6, | 2, | 2, | 2, | 2 |
| $D:$ | 5, | 5, | 5, | 1, | 1, | 1 |
Результат броска каждой из кости из набора больше результата бросания следующей кости с вероятностью $2/3$:
${\displaystyle P(A>B)=P(B>C)=P(C>D)=P(D>A)={2 \over 3}}$
Результат бросания кости $B$ определен заранее; кость $A$ превысит этот результат в $2/3$ случаев, поскольку числа на четырёх из шести его граней больше.
Аналогично, кость $B$ превысит результат $C$ с вероятностью $2/3$, поскольку у $C$ только на двух гранях числа большие.
$P(C>D)$ согласно результатам составления условных вероятностей двух событий:
При бросании $C$ выпадает $6$ (вероятность $1/3$); $C$ дает больший результат, независимо от результата бросания $D$ (вероятность $1$).
При бросании $C$ выпадает $2$ (вероятность $2/3$); $C$ дает больший результат, за исключением получения $5$ при бросании $D$ (вероятность $1/2$).
Суммарная вероятность выигрыша $C$, таким образом, составляет:
${\displaystyle \left({1 \over 3}\times 1\right)+\left({2 \over 3}\times {1 \over 2}\right)={2 \over 3}}$.
Аналогичным образом вероятность выигрыша при бросании $D$ по сравнению с бросанием $A$ составляет:
${\displaystyle \left({1 \over 2}\times 1\right)+\left({1 \over 2}\times {1 \over 3}\right)={2 \over 3}}$.
Четыре кости из набора Эфрона, впрочем, имеют разные вероятности выигрыша в игре против кости, выбранной случайным образом из оставшихся трех.
Согласно расчётам выше, бросание кости $A$ дает больший результат, чем бросание кости $B$, в двух третях случаев. Впрочем, $A$ может победить $D$ только в каждом третьем случае. Вероятность же лучшего результата при бросании $A$ по сравнению с бросанием $C$ составляет $4/9$ (на $A$ должно выпасть $4$ и на $C$ должно выпасть $2$). Таким образом общая вероятность получения большего числа при бросании $A$ , чем при бросании другой кости, выбранной случайным образом:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{4 \over 9}\right)={13 \over 27}}$.
Аналогично, $B$ побеждает $C$ с вероятностью $2/3$ и может победить $A$ в $1/3$ случаев. Вероятность для кости $B$ дать при бросании результат больший, чем при бросании кости $D$, составляет $1/2$ (вероятность выпадения $1$ на кубике $D$). Таким образом, вероятность победы $B$ над другой костью из набора:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{1 \over 2}\right)={1 \over 2}}$.
Кость $C$ побеждает $D$ в двух третях случаев и имеет вероятность $1/3$ выигрыша у кубика $B$. Вероятность её выигрыша у кубика $A$ составляет $5/9$. Совокупная вероятность победы $C$ над выбранным случайным образом «соперником»:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{5 \over 9}\right)={14 \over 27}}$.
Наконец, $D$ в $2/3$ случаев побеждает $A$ и в $1/3$ случаев побеждает $C$. Вероятность, что результат броска этой кости превысит результат бросания $B$, составляет $1/2$ (вероятность выпадения $5$ на $D$). Поэтому $D$ даст результат, больший, чем у выбранной случайным образом кости с вероятностью:
${\displaystyle {1 \over 3}\times \left({2 \over 3}+{1 \over 3}+{1 \over 2}\right)={1 \over 2}}$.
Таким образом, кость $C$ является наилучшей из набора с точки зрения вероятности выпадения числа, большего чем результат бросания любой другой кости из набора. Для неё такая вероятность составляет $0,5185$. Кость $C$ также характеризуется наибольшим математическим ожиданием результата бросания — $31⁄3$ (для $A$ оно составляет $22⁄3$, а для $B$ и $D$ равно $3$).
Хомячковый рай. Уйти и потеряться:
Рост спроса в некоторых отраслях. Жизнь продолжается!

Хомячковый рай. Уйти и потеряться:
Как сделать предохранитель

Чего только не суют иные вместо предохранителей. Мне однажды пришлось из предохранительной колодки вытаскивать гвоздь! А ведь у любого найдется кусочек провода, чтоб изготовить предохранитель! Мне как-то на глаза попалась таблица, которую я предлагаю вам - по ней вы можете выбрать диаметр проволочки, чтобы сделать предохранитель.
Ток, А Диаметр провода в мм Ток, А Диаметр провода в мм Медь Алюм. Сталь Олово Медь Алюм. Сталь Олово 1 0,039 0,066 0,132 0,183 60 0,82 1,0 1,8 2,8 2 0,069 0,104 0,189 0,285 70 0,91 1,1 2,0 3,1 3 0,107 0,137 0,245 0,380 80 1,0 1,22 2,2 3,4 5 0,18 0,193 0,346 0,53 90 1,08 1,32 2,38 3,65 7 0,203 0,250 0,45 0,66 100 1,15 1,42 2,55 3,9 10 0,250 0,305 0,55 0,85 120 1,31 1,60 2,85 4,45 15 0,32 0,40 0,72 1,02 160 1,57 1,94 3,2 4,9 20 0,39 0,485 0,87 1,33 180 1,72 2,10 3,7 5,8 25 0,46 0,56 1,0 1,56 200 1,84 2,25 4,05 6,2 30 0,52 0,64 1,15 1,77 225 1,99 2,45 4,4 6,75 35 0,58 0,70 1,26 1,95 250 2,14 2,60 4,7 7,25 40 0,63 0,77 1,38 2,14 275 2,2 2,80 5,0 7,7 45 0,68 0,83 1,5 2,3 300 2,4 2,95 5,3 8,2 50 0,73 0,89 1,6 2,45
Хомячковый рай. Уйти и потеряться:
Эксперимент с Mathjax - проверка вставки формулы
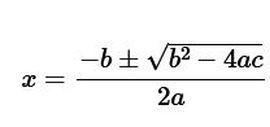
Ввод формулы
Если $a \ne 0$, то существует 2 решения
квадратного уравнения \(ax^2 + bx + c = 0\)
Вот они:
$$x = {-b \pm \sqrt{\texttip{b^2-4ac}
{descriminant}} \over 2a}.$$
Если $a \ne 0$, то существует 2 решения квадратного уравнения $ax^2 + bx + c = 0$
Вот они: $$x = {-b \pm \sqrt{\texttip{b^2-4ac}{descriminant}} \over 2a}.$$