Алгоритм построения набора нетранзитивных игральных костей
Нетранзитивными игральными костями я заинтересовался, когда увидел задачу Нетранзитивные кубики на Элементах. Приведенное на сайте решение меня абсолютно не удовлетворило (собственно это и решением назвать нельзя: автор просто выдал готовый ответ). Послесловие оказалось не лучше, что только подстегнуло интерес к задаче.
Остались вопросы. Можно ли построить набор кубиков "с нуля"? Как построить набор костей с другим количеством граней? Будут ли там решения с равными вероятностями выигрыша? Я попытался найти общий алгоритм со следующими условиями:
- Алгоритм должен работать для любого количества костей с любым количеством граней (равным для всех костей в наборе).
- Все кости выигрывают у своего соседа в наборе с равной вероятностью.
- Алгоритм должен создавать набор для любой заданной вероятности выигрыша.
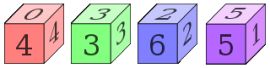
Для демонстрации идеи возьмем следующий нетранзитивный набор из 4-х кубиков:
| A: | 1 | 2 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|
| B: | 3 | 4 | 5 | 20 | 21 | 22 |
| C: | 6 | 7 | 8 | 9 | 23 | 24 |
| D: | 10 | 11 | 12 | 13 | 14 | 15 |
В этом наборе $A < B < C < D < A$ с вероятностью $24/36$. Представим его в следующем виде:
| A | A | B | B | B | C | C | C | C | D | D | D | D | D | D | A | A | A | A | B | B | B | C | C |
Здесь порядковый номер символа равен числу на соответствующей кости. Теперь можно абстрагироваться от конкретных чисел и сравнивать расположение символов относительно друг друга. Например количество пар $A$ и $B$, в которых $A$ стоит слева от $B$ (т.е. $A < B$) равно $24$. Эти пары соответствуют элементарным исходам бросков костей $A$ и $B$, в которых выигрывает кубик $B$, что и дает вероятность выигрыша $24/36$.
Итак, чтобы построить нетранзитивный набор костей, нужно найти такую перестановку символов, в которой количество пар $X < Y$ одинаково для всех соседних в наборе костей и соответствует искомой вероятности. Как это сделать?
Перестановку можно получить из таблиц выигрышей. Для рассмотренного выше набора они выглядят так:
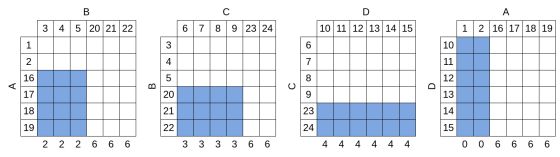
Закрашенные ячейки соответствуют исходам, в которых кубик проигрывает соседу слева (назовём их "проигрышными ячейками"). Числа под таблицей показывают расположение в перестановке символа кубика относительно символов его соседа слева. Например, из таблицы AB следует, что первый, второй и третий символы B стоят после второго символа A, а четвёртый, пятый и шестой B - после шестого A. Чтобы получить перестановку для нетранзитивного набора, возьмем следующую перестановку:
| A | A | A | A | A | A | B | B | B | B | B | B | C | C | C | C | C | C | D | D | D | D | D | D |
и будем последовательно сдвигать символы в соответствии с таблицами выигрышей:
| A | A | B | B | B | A | A | A | A | B | B | B | C | C | C | C | C | C | D | D | D | D | D | D |
| A | A | B | B | B | C | C | C | C | A | A | A | A | B | B | B | C | C | D | D | D | D | D | D |
| A | A | B | B | B | C | C | C | C | D | D | D | D | D | D | A | A | A | A | B | B | B | C | C |
Замечу, что вообще из таблицы выигрышей нельзя однозначно получить перестановку. Например, двум перестановкам:
| A | A | D | C | D | B | C | B | B | B | C | C | D | D | A | D | C | A | A | B | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | A | D | C | B | D | C | B | B | B | C | C | D | D | A | D | A | A | C | B | A | B | C | D |
соответствуют одни и те же таблицы выигрышей. Но нам важно лишь, что в обоих наборах будет одна и та же вероятность выигрыша.
Теперь самое сложное: нужно построить таблицы выигрышей, соответствующие искомому нетранзитивному набору костей. Набор таких таблиц должен удовлетворять некоторым условиям, которые мы сейчас сформулируем:
Выберем на каждой игральной кости по одной грани. Этим граням будут соответствовать ячейки в таблицах выигрышей (по одной в каждой таблице) такие, что номер столбца ячейки в одной таблице будет равен номеру строки ячейки в следующей таблице. Например, для рассмотренного выше набора 4-х кубиков это выглядит так:
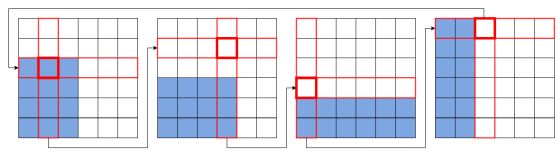
Очевидно, что в любом таком наборе ячейки не могут быть все выигрышными или все проигрышными.
Далее рассмотрим наборы ячеек, состоящие только из ячеек на главной диагонали таблицы - в каждом таком наборе у всех ячеек будут совпадать номера строк и столбцов. Так как все ячейки в наборе не могут быть выигрышными, то для каждой ячейки на главной диагонали в наборе таблиц выигрышей должна быть хотя бы одна таблица, в которой эта ячейка будет проигрышной (и хотя бы одна таблица, в которой эта ячейка будет выигрышной).
Второе условие также дает ограничение на максимальную вероятность выигрыша. Для костей с четным количеством граней минимальная площадь проигрышной области будет у прямоугольника с одной из двух центральных ячеек главной диагонали в правом верхнем углу. Для костей с нечетным количеством граней это будет квадрат с центральной ячейкой в правом верхнем углу. Т.е. максимальная вероятность выигрыша равна для костей с четным количеством граней:
$$1 - {s \over 2}{({s \over 2} + 1)} \over s^2$$и для костей с нечетным количеством граней:
$$1 - {{({{s + 1} \over 2})}^2} \over s^2$$где s - количество граней.
Теперь на нескольких примерах покажем как построить таблицы выигрышей, удовлетворяющие этим условиям:
Начнем с нашего примера из четырёх кубиков с вероятностью выигрыша $24/36$. Область проигрышных ячеек во всех таблицах будет иметь форму прямоугольника. В 1-й таблице высота этого прямоугольника будет равна высоте таблицы. В каждой следующей таблице высота прямоугольника будет убывать так, чтобы $h_{i} = s - w_{i-1}$, где $h_{i}$ и $w_{i}$- высота и ширина прямоугольника в i-й таблице:
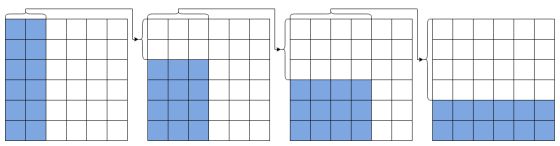
В этом примере хорошо видно, что все наборы ячеек удовлетворяют первому условию.
Добавим в искомый набор несколько кубиков. Тогда в наборе таблиц выше нужно продублировать любую таблицу до нужного количества кубиков, соблюдая порядок убывания высоты прямоугольников с проигрышными ячейками. Например, для набора из 6 кубиков таблицы выигрышей могут выглядеть так:
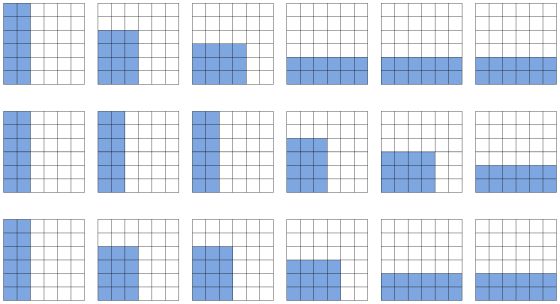
Следующий пример - 4 кубика с вероятностью $21/36$. Также разместим проигрышные ячейки в прямоугольные области убывающей высоты (на рисунке закрашены синим). Оставшиеся проигрышные ячейки (закрашены зеленым), не вошедшие в основную прямоугольную область, разместим так: во всех таблицах, кроме последней - столбцом справа от прямоугольника, в последней таблице - в несколько столбцов над прямоугольником:
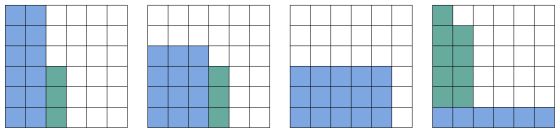
Уберём из последнего набора один кубик. При текущем способе построения таблиц выигрышей мы не можем получить таблицу, в которой область проигрышных ячеек покрывает правую нижнюю ячейку таблицы. Исправим это. Разместим в 1-й таблице проигрышные ячейки в две прямоугольные области: высота первой так же равна высоте таблицы, а ширина второй (закрашена фиолетовым) дополняет ширину первой до ширины таблицы. Оставшиеся ячейки разместим в столбец справа от первой области и над второй:
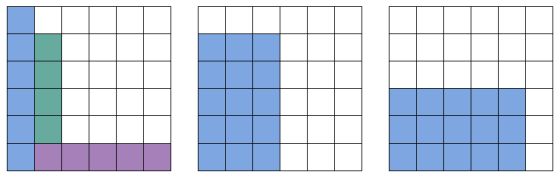
Для наборов с большим количеством граней и малым количеством костей высота второго прямоугольника в 1-й таблице может быть несколько строк, но не больше ширины первого прямоугольника. Этот параметр нужно найти перебором - чтобы ширина прямоугольника в последней таблице равнялась ширине таблицы за вычетом высоты второго прямоугольника в 1-й таблице. Например, для набора из трех 14-гранников с вероятностью $119/196$ таблицы выигрышей выглядят так:

Наконец, рассмотрим пример из трёх кубиков с вероятностью $19/36$. В 1-й таблице столбец проигрышных ячеек, не вошедших в основной прямоугольник, не может быть выше главной диагонали. На рисунке ниже красным показаны 3 набора ячеек, в каждом из которых все ячейки являются проигрышными, что противоречит первому условию:
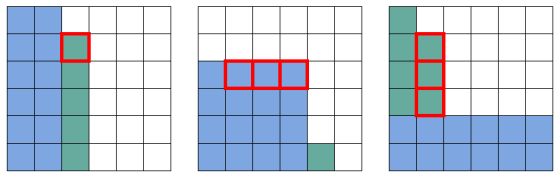
В этом случае следует сразу начать с размещения в 1-й таблице проигрышных ячеек в два прямоугольника:
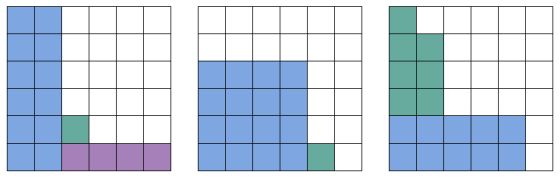
Если описанным выше способом не удается построить набор таблиц выигрышей - значит, для заданного количества костей и граней искомая вероятность выигрыша недостижима. Например, из трех кубиков нельзя построить нетранзитивный набор с вероятностью выигрыша больше, чем $21/36$.
Ссылка на реализацию алгоритма.Автор: Артур Урманов
Хомячковый рай. Уйти и потеряться:
Метанетранзитивные кости Алексея Лебедева
Многим наверняка известны такие парадоксальные объекты, как нетранзитивные игральные кости: игральный кубик $А$ чаще побеждает $В$, чем проигрывает ему; кубик $В$ чаще побеждает $С$, чем проигрывает ему; но кубик $С$ чаще побеждает $А$, чем проигрывает ему, — по принципу игры «Камень, ножницы, бумага». По мнению Мартина Гарднера, нетранзитивные игральные кости «позволяют глубже осознать значение недавних открытий, связанных с общим классом вероятностных парадоксов, в которых нарушается правило транзитивности. С помощью любого из этих наборов игральных костей вы можете держать пари в условиях, настолько противоречащих интуиции, что опытные игроки почти не в состоянии разобраться в них, даже если они полностью проанализируют ход игры».
Изобретено уже немало наборов нетранзитивных костей, обладающих разными свойствами. Это кости Брэдлм Эфрона, изначально описанные Мартином Гарднером; кости Т. Бирдон с числами $\pi$, $e$, $\phi$; кости Дж. Грайма, такие, что при удвоении набора (игрок бросает две одинаковые кости одновременно) меняется направление «битья» (если в одинарном наборе $A > B > C >A$, то в двойном $AA < BB < CC < AA$; кости О. ван Девентера для игры втроем (какие бы кости ни выбрали первые два игрока, третий всегда может выбрать такую, которая будет чаще «бить» первые две, чем проигрывать им); кости для игры вчетвером Э. Пегга мл. и т. д.
Все эти разные наборы нетранзитивных костей можно сравнить друг с другом и однозначно линейно упорядочить по степени нетранзитивности: есть наборы, в которых она выражена слабо (кости побеждают друг друга с вероятностью чуть больше 50%), и есть наборы, в которых она выражена сильно(кости побеждают друг друга с вероятностью до 75% — это доказанный предел). Иными словами, наборы нетранзитивных костей можно упорядочить строго транзитивно.
Александр Поддьяков, доктор психологических наук, профессор НИУ ВШЭ, главный научный сотрудник ИП РАН ввёл понятие «метанетранзитивность». Он поставил вопрос: возможны ли метанетранзитивные системы? В каждой из таких систем есть нетранзитивные циклы превосходств, но и сами эти системы образуют свои нетранзитивные циклы.
Оказалось, что да — такие системы есть.
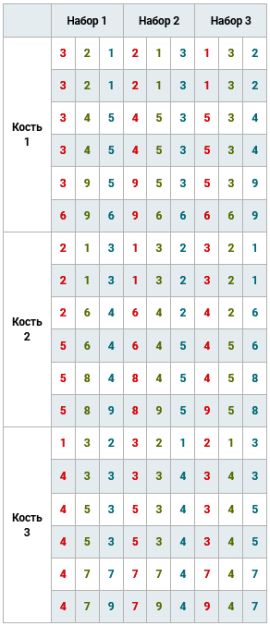
Алексей Лебедев, доктор физико-математических наук, доцент МГУ, автор публикаций по совершенно новой теме — изучение нетранзитивностей непрерывных распределений, создал новый вариант нетранзитивных костей. Это метанетранзитивные кости (метакости): три набора костей, в каждом из которых кости образуют свой нетранзитивный круг, а отношения между тремя наборами тоже нетранзитивны.
Устроены они так (далее цитирую Алексея Лебедева). «На каждой грани кости пишется не одно, а три числа: красное, зеленое и синее. После каждого броска костей игрок получает фишку соответствующего цвета, если у него выпало красное, синее или зеленое число больше, чем у противника (это не взаимно исключающие случаи, больше могут быть одновременно два или все три числа). Считаем, что одна кость превосходит другую, если средние выигрыши по всем цветам фишек больше $1/2$. Выигрышности набора костей считаем отдельно по каждому цвету (т.е., это три числа). Считаем, что один набор костей превосходит другой, если он превосходит его по выигрышностям хотя бы для двух цветов.
Таким образом, каждый набор получается нетранзитивным, и набор этих наборов тоже нетранзитивен (в смысле введенных отношений превосходства на костях и наборах)».
Хомячковый рай. Уйти и потеряться:
Взлёты и падения чисел-градин

| В МИРЕ НАУКИ Scientific American · Издание на русском языке № 3 · МАРТ 1984 · С. 102-107 |
БРАЙАН ХЭЙЕС
Пешеход, делающий три шага вперёд и два назад, хотя и не быстро, но всё же доберётся до цели. А вот в одной любопытной нерешённой задаче из теории чисел утверждается, что при таком передвижении достижение цели весьма сомнительно. Задача формулируется так. Возьмём произвольное целое число N больше нуля (любое натуральное число). Если оно нечётное, умножим его
Если задано конкретное N, то для ответа на поставленные вопросы достаточно обычной арифметики. Например, начав с нечётного числа 27, следующим получим значение
Трудность задачи заключается не в выписывании последовательности для данного N, а в нахождении общего решения, которое годилось бы для всех исходных значений N. Такое общее решение пока не получено. Было испробовано огромное количество чисел, и все они вели себя одинаково, но ещё никто не смог доказать, что так же будет с любым целым числом. Из нерешённых задач теории чисел - эта едва ли самая важная, но она одна из тех, что вызывают сильную досаду. И описание вычислительной процедуры, и её выполнение чрезвычайно просты, но понять, к чему она может привести, невероятно трудно.
На примере этой задачи особенно хорошо видны как польза компьютера при вычислениях, так и ограниченность его возможностей. С небольшими целыми числами можно справиться самим, а далее для вычислений понадобится механический помощник. Им может быть любая машина, даже небольшой программируемый калькулятор. В области же очень больших чисел такая работа под силу только самым мощным ЭВМ. Когда же ставятся более глубокие вопросы, уже не поможет никакой компьютер. Основное назначение ЭВМ - быть подспорьем в математическом эксперименте: строить примеры и контрпримеры. Для описания же закона, по которому N изменяет свои значения, нужна не числодробилка, а скорее механический <доказыватель теорем>.
Если к произвольному целому числу N многократно применять описанные преобразования, то какого результата следует ожидать? На этот счёт есть три интуитивные гипотезы.
В первой гипотезе рассуждаем так. Имеется равное количество чётных и нечётных чисел, так что в любой длинной последовательности вычислений чётные и нечётные N будут появляться одинаково часто. Нечётное N увеличивается втрое (чуть больше), а чётное уменьшается всего лишь вдвое. Следовательно, по мере роста числа итераций значение N будет бесконечно возрастать. За каждую итерацию N будет в среднем увеличиваться на
Вторая гипотеза основана на тезисе <Чем выше заберёшься, тем ниже скатишься>. Справедливость этой мысли подкрепляется тем реальным фактом, что стoит в вычислениях получить точную степень двойки, как последовательность неудержимо скатится
Третья гипотеза по форме схожа со второй, но приводит к иному выводу. Замечено, что как только вычисления меняют направление, скажем после ряда чётных чисел появляется нечётное, мы вновь возвращаемся в ту же область, в которой были раньше. В самом деле, получая то бoльшие, то меньшие числа, мы можем сколь угодно часто возвращаться в некую конечную область. Можно ожидать, что рано или поздно результат вычислений повторится, и, как только это произойдёт, всё дальнейшее предрешено. Образуется замкнутый цикл, из которого уже никогда не выйти. Это объясняется тем, что выбор каждого следующего шага происходит по вполне определённому правилу.
К рассмотренным гипотезам не следует относиться слишком серьёзно: они не могут быть все справедливыми.
Делая эти оговорки, должен тем не менее отметить, что все три гипотезы считаю в высшей степени правдоподобными. Взвешивая каждую из них, я думаю, что не может быть сомнений в её справедливости, и в то же время другие гипотезы мне кажутся не менее убедительными. Что же по этому поводу говорит математический эксперимент?
Начнём вычисления с 1. Это - нечётное число, поэтому, следуя условиям задачи, умножим его
Из всех натуральных чисел единица занимает особое положение: это первое число и наименьшее. Таким образом, результат, полученный для
После исследования первых четырёх натуральных чисел вроде бы выявилась определённая тенденция, но всё же оснований для окончательного вывода нет. В проведённых вычислениях нас больше всего интересуют две величины: максимальное из полученных значений N и длина пути, под которой будем понимать общее число итераций, необходимое для
Снова вернёмся к последовательности, которая порождается начальным
Но если вычисления продолжить, метод <три шага вперёд и два назад> приводит к осциллирующей кривой с постоянно возрастающей амплитудой. Новыми пиками будут 142, 214, 322
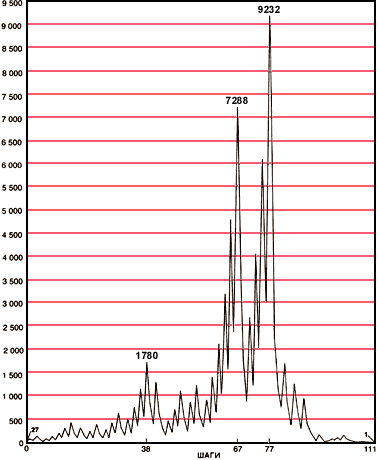
Последовательность значений
Подобные вычисления проводились с огромным набором целых чисел. Сотрудник Токийского университета Набуо Йонеда исследовал все целые числа
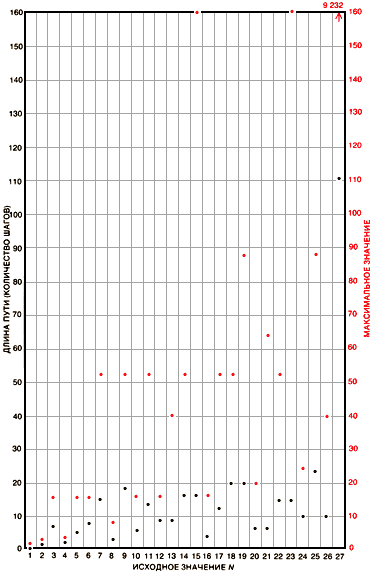
Последовательный перечень самых длинных путей для N от 1 до 100 000 |
Последовательный перечень максимумов для N от 1 до 100 000 |
История проблемы
Лагариас ссылается примерно на 20 научных статей по проблеме
Группой исследователей из Лаборатории искусственного интеллекта Массачусетского технологического института в начале
Постоянно кочуя, задача обрастала множеством имён. Название <проблема
На языке высокого уровня, скажем на Бейсике, можно написать программу для вычисления
IF N MOD 2 = 0 THEN N = N/2 ELSE N = 3*N + 1
Первой здесь записана операция, которую люди (но не машина) выполняют, не прибегая к явным вычислениям: определение чётности (или нечётности) числа N. Компьютер пользуется для этого операцией сравнения по
Такая программа на Бейсике вполне сносно справляется с порождением
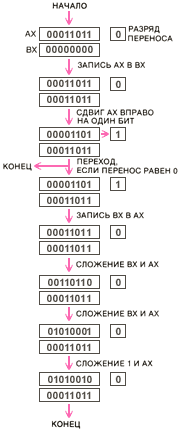
Алгоритм получения
Приблизительное представление о такой программе на языке машины даёт рисунок справа. Предполагается, что исходное значение N первоначально находится в
На первом шаге исходное число в двоичном коде переписывается в другой регистр, обозначенный на
Если N чётное, то вычисления на этом этапе закончены. В
Из рисунка видно, что регистры имеют 8 разрядов и, следовательно, в них нельзя поместить число больше
Алгоритм получения одного значения N - всего лишь фрагмент рабочей программы. В ней, кроме того, должна быть предусмотрена возможность ввода в машину значений и вывода результатов. Реальные же программы для исследования поведения
Разновидности формулы 3N+1, в которых используются другие коэффициенты и постоянные, также плохо поддаются исследованию. У. Госпер и Р. Шоппель, когда они ещё входили в группу HAKMEM, исследовали проблему
Программу, позволяющую лишь выявить числа, которые не попадают в цикл
После всего, что было сказано, по-видимому, нет смысла продолжать поиски числа, которое вело бы себя
Возможно, самые интригующие свойства таких чисел - это выраженный характер распределения максимальных значений и длин пути. Если такое небольшое число, как 27, удерживается <в подвешенном состоянии> в течение 111 шагов и достигает максимума 9232, то можно было бы ожидать, что длина пути и максимальные значения растут так же быстро, как
Среди первой сотни целых чисел самый длинный путь равен 118 шагам
Легко видеть, что максимальные значения, получаемые при вычислении чисел-градин, неизменно чётные. Можно также доказать, что лишь нечётное N способно установить новый рекорд максимального значения (за исключением
Полученная на ЭВМ распечатка длин пути и максимумов для некоторой области целых чисел представляет собой удручающую смесь закономерности и беспорядка. Последовательность безусловно не случайна, но ей не удаётся дать никакого толкования. Например, некоторые максимальные значения повторяются чаще, чем другие, причём появление некоторых максимумов настолько часто, что их нельзя описать
Распределение длины пути столь же хаотично. Можно породить любую из возможных длин пути (последовательностью точных степеней двойки), но и в этом случае некоторые числа будут появляться чаще других. Кроме того, и длины пути, и максимумы проявляют чёткую тенденцию к группированию в кластеры. Ф. Грюнберг из Калифорнийского университета в Нотридже в 1976 году опубликовал перечень таких кластеров. Самый обширный из них представлял собой цепочку из 52 целых чисел, которые проходили одинаково длинный путь. Возникает вопрос: могут ли одинаковые максимумы и одинаковые длины пути достигаться двумя последовательными числами? Ответ на этот вопрос можно дать в алгебраической форме, но если читатель предпочитает демонстрацию на примерах с числами, ему следует рассмотреть последовательности для всех N от 386
Один из подходов, позволяющих пролить свет на задачу о градинах, состоит в обратной её постановке. Предположим, что все положительные целые числа действительно обязательно попадут в цикл
Этот метод прекрасно бы подошёл для получения общего решения задачи о градинах, если бы только его можно было довести до конца. Оказывается, процедура не столь прямолинейна, как кажется. Обычная функция преобразования градин однозначна: у любого значения N в любой точке вычислений только один преемник. Если, например,
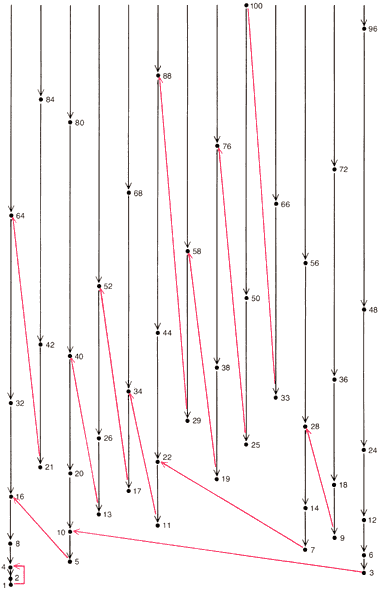
Дерево, порождённое
Такого рода разветвляющуюся систему можно проследить только до определённого уровня. Движемся по отдельной ветви до некоторого наперёд заданного предела и затем переключаем внимание на другую ветвь. При пределе 100 надо будет изучить 13 ветвей, причём в этой числовой системе ручейков и протоков между собой связаны